library(dplyr)
library(ggplot2)
library(readr)
library(rstan)
c_orange_dark <- "#e76f51"
c_orange_light <- "#f4a261"
c_yellow <- "#e9c46a"
c_green_blue <-"#2a9d8f"
c_blue_dark <- "#264653"
c_lightblue <- "#219ebc"18 - Regresión lineal con {RStan} (Clima en Australia)
En este artículo se muestra como implementar en R y {RStan} algunos de los modelos necesarios en el ejercicio Clima en Australia de la Práctica 4.
Comenzamos cargando las liberías que vamos a usar.
df <- read_csv(
"https://raw.githubusercontent.com/ee-unr/estadistica-bayesiana/main/datos/weather_WU.csv"
)
# Explorar los datos
ggplot(df) +
geom_point(aes(x = temp9am, y = temp3pm, color = location), alpha = 0.7, size = 2) +
scale_color_manual(values = c(c_orange_dark, c_green_blue)) +
labs(
x = "Temperatura a las 9 a.m. (C°)",
y = "Temperatura a las 3 p.m. (C°)",
color = "Ciudad"
) +
theme_bw()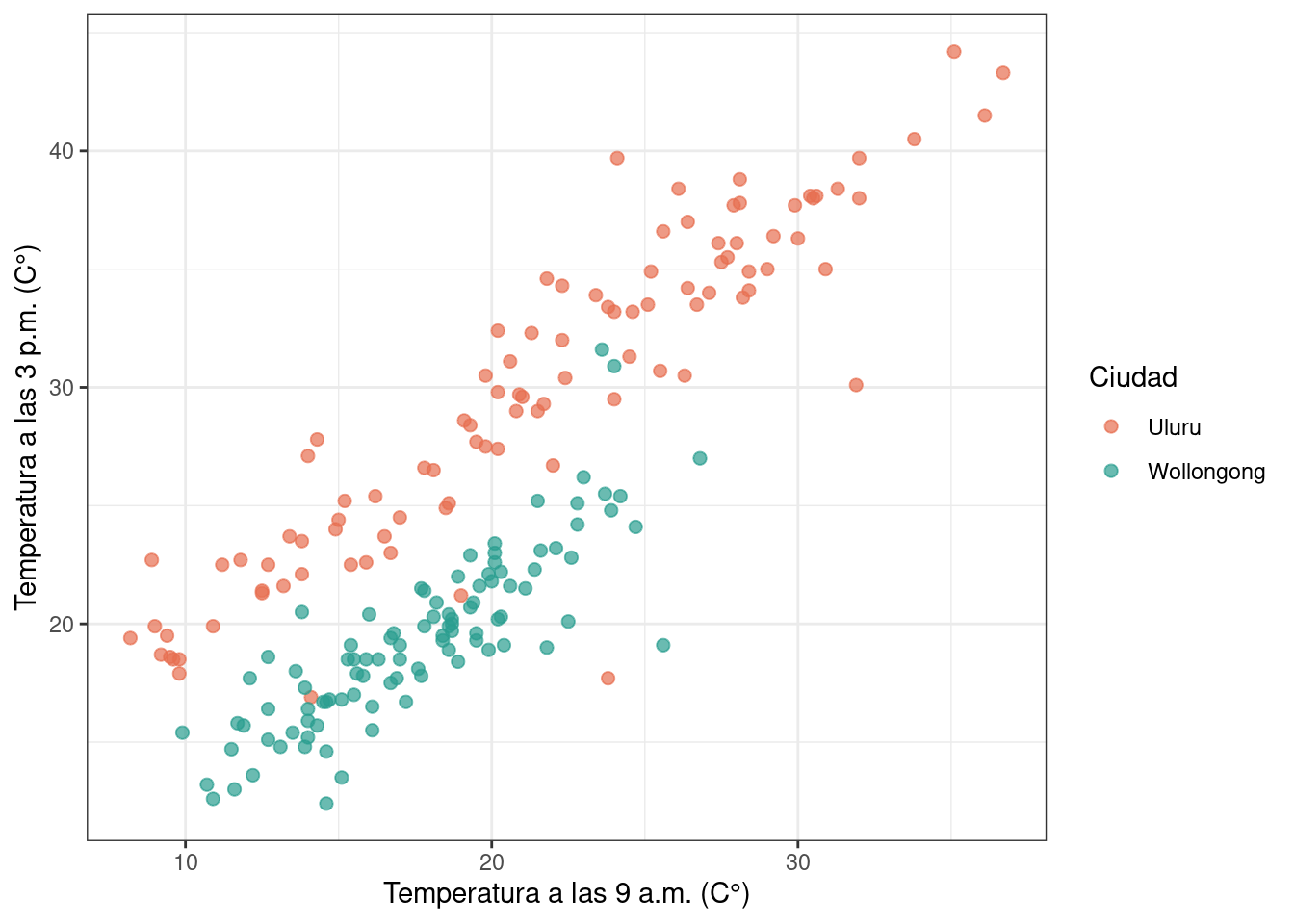
Modelos
A continuación se presentan los modelos que se consideran en el ejercicio. En todos los casos se tiene:
- \(Y_i\): temperatura a las 3 p.m. de la observación i-ésima.
- \(X_i\): temperatura a las 9 a.m. de la observacion i-ésima.
Modelo 1
\[ \begin{aligned} Y_i \mid \mu_i, \sigma &\underset{iid}{\sim} \text{Normal}(\mu_i, \sigma) \\ \mu_i &= \beta_0 + \beta_1 x_i \\ \beta_0 &\sim \text{Normal} \\ \beta_1 &\sim \text{Normal} \\ \sigma &\sim \text{Normal}^+ \\ \end{aligned} \]
Modelo 2
\[ \begin{aligned} Y_i \mid \mu_i, \sigma &\underset{iid}{\sim}\text{Normal}(\mu_i, \sigma) \\ \mu_i &= \beta_{0, j[i]} \\ \beta_{0, j} &\sim \text{Normal} \quad \forall j = 1, 2 \\ \sigma &\sim \text{Normal}^+ \\ \end{aligned} \]
donde \(j\) indexa a las diferentes ciudades.
Para pensar: ¿qué indican \(\beta_{0, 1}\) y \(\beta_{0, 2}\)?
Modelo 3
\[ \begin{aligned} Y_i \mid \mu_i, \sigma &\underset{iid}{\sim} \text{Normal}(\mu_i, \sigma) \\ \mu_i &= \beta_{0, j[i]} + \beta_1 x_i \\ \beta_{0, j} &\sim \text{Normal} \quad \forall j = 1, 2 \\ \beta_1 &\sim \text{Normal} \\ \sigma &\sim \text{Normal}^+ \\ \end{aligned} \]
Para pensar: ¿en qué difieren los \(\beta_{0, 1}\) y \(\beta_{0, 2}\) de este modelo con los del modelo 2? ¿Y en qué difiere \(\beta_1\) de este modelo con el del modelo 1?
Modelo 4
\[ \begin{aligned} Y_i \mid \mu_i, \sigma &\underset{iid}{\sim} \text{Normal}(\mu_i, \sigma) \\ \mu_i &= \beta_{0, j[i]} + \beta_{1, j[i]} x_i \\ \beta_{0, j} &\sim \text{Normal} \quad \forall j = 1, 2 \\ \beta_{1, j} &\sim \text{Normal} \quad \forall j = 1, 2 \\ \sigma &\sim \text{Normal}^+ \\ \end{aligned} \]
Implementación
Modelo 1
stan/australia/modelo_1.stan
data {
int<lower=0> N; // Cantidad de observaciones
vector[N] temp9am; // Temperatura a las 9 am (predictor)
vector[N] temp3pm; // Temperatura a las 3 pm (respuesta)
}
parameters {
real beta0; // Intercepto
real beta1; // Pendiente
real<lower=0> sigma; // Desvío estándar del error
}
transformed parameters {
vector[N] mu; // Predictor lineal
mu = beta0 + beta1 * temp9am;
}
model {
beta0 ~ normal(17.5, 6.25);
beta1 ~ normal(0, 10);
sigma ~ normal(0, 15);
temp3pm ~ normal(mu, sigma);
}
generated quantities {
vector[N] y_rep;
vector[N] log_likelihood;
for (i in 1:N) {
// Obtención de muestras de la distribución predictiva a posteriori
y_rep[i] = normal_rng(mu[i], sigma);
// Cálculo de la log-verosimilitud
log_likelihood[i] = normal_lpdf(temp3pm[i] | mu[i], sigma);
}
}# Datos que pasamos a Stan
stan_data_1 <- list(
N = nrow(df),
temp9am = df$temp9am,
temp3pm = df$temp3pm
)
ruta_modelo_1 <- here::here(
"recursos", "codigo", "stan", "australia", "modelo_1.stan"
)
modelo_1 <- stan_model(file = ruta_modelo_1)
modelo_1_fit <- sampling(
modelo_1, # El modelo
data = stan_data_1, # Datos
chains = 4, # Cantidad de cadenas
seed = 1211, # Para que el resultado sea reproducible
refresh = 0, # Mostrar mensajes del sampler (0: no)
)
# Convertimos las muestras a data.frame, conservando solo los parámetros de interés
df_draws_1 <- as.data.frame(extract(modelo_1_fit, c("beta0", "beta1", "sigma")))Graficamos la distribución a posteriori marginal de los parámetros.
df_draws_long_1 <- df_draws_1 |>
tidyr::pivot_longer(c("beta0", "beta1", "sigma"), names_to = "parametro")
ggplot(df_draws_long_1) +
geom_histogram(
aes(x = value, y = after_stat(density)),
bins = 30,
fill = c_orange_light,
color = c_orange_light
) +
facet_wrap(~ parametro, scales = "free") +
labs(x = "Valor", y = "Densidad") +
theme_bw()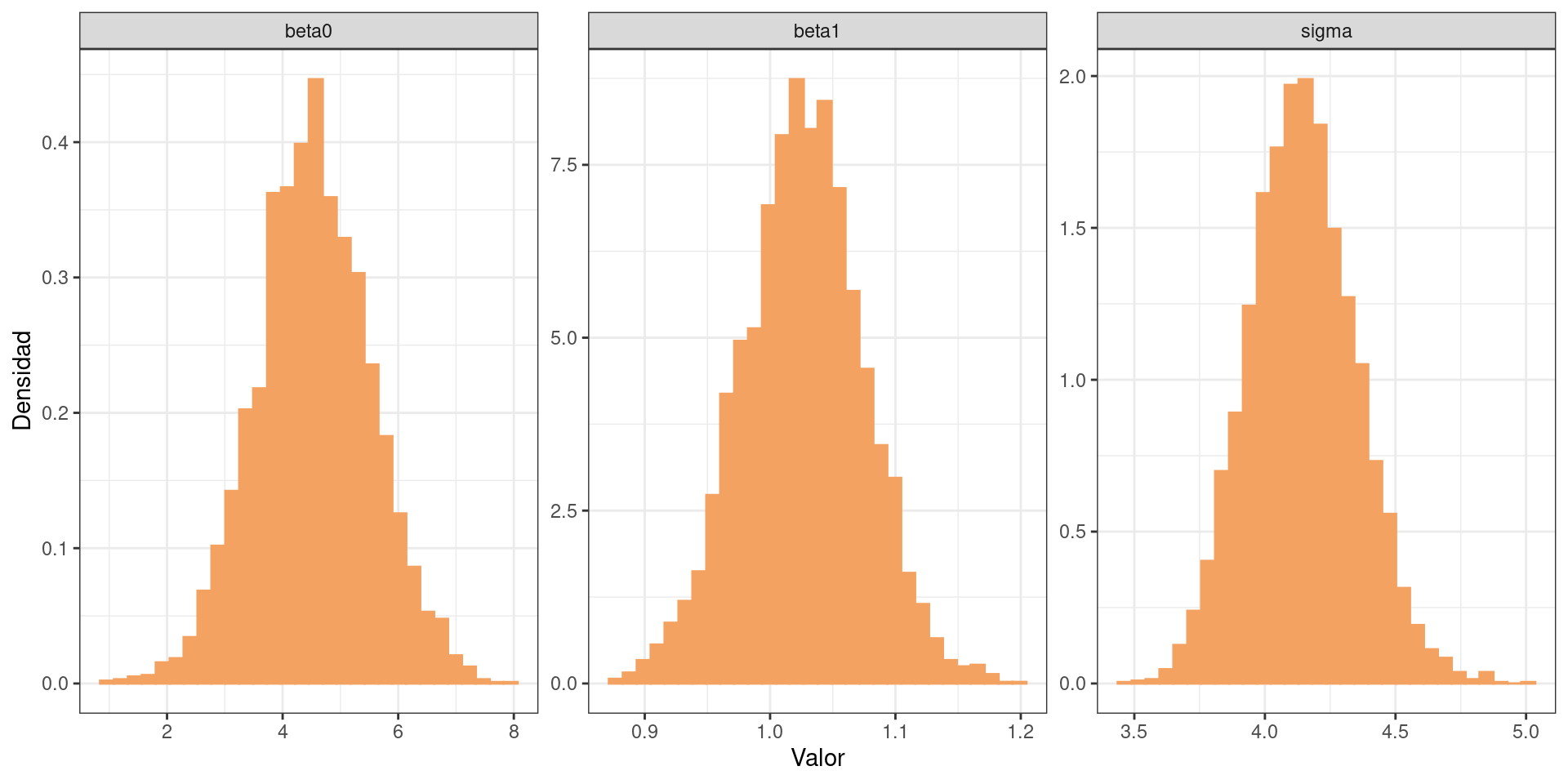
La recta de regresión está dada por un intercepto y una pendiente. Al contar con múltiples valores de interceptos y pendientes, es posible pensar que se tienen múltiples muestras de rectas de regresión. Para graficar algunas de estas rectas simplemente seleccionamos algunos de los pares de (beta0, beta1) que se obtuvieron del posterior.
ggplot(df) +
geom_point(aes(x = temp9am, y = temp3pm, color = location), alpha = 0.7, size = 2) +
geom_abline(
aes(intercept = beta0, slope = beta1),
alpha = 0.3,
color = "gray30",
data = df_draws_1[sample(4000, 40), ]
) +
scale_color_manual(values = c(c_orange_dark, c_green_blue)) +
labs(
x = "Temperatura a las 9 a.m. (C°)",
y = "Temperatura a las 3 p.m. (C°)",
color = "Ciudad"
) +
theme_bw()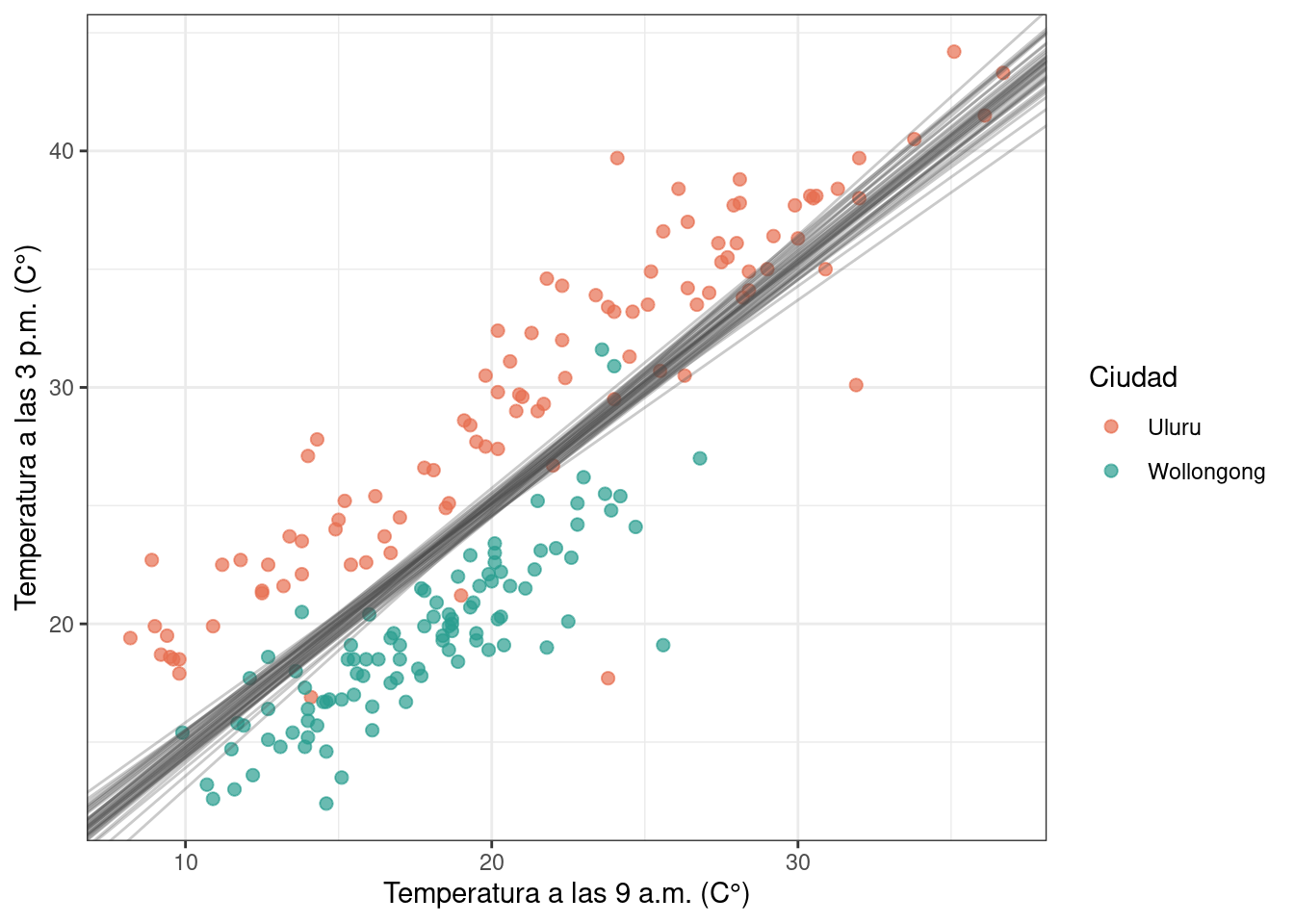
También es posible obtener muestras de la distribución predictiva a posteriori para una grilla de valores de temp9am, resumirla mediante un intervalo de credibilidad del 95%, y superponerla en el gráfico anterior.
n_muestras <- 4000
n_grilla <- 200
temp9am_seq <- seq(min(df$temp9am), max(df$temp9am), length.out = n_grilla)
y_pp_matriz <- matrix(nrow = n_muestras, ncol = n_grilla)
for (j in seq_len(n_grilla)) {
mu <- df_draws_1$beta0 + df_draws_1$beta1 * temp9am_seq[j] # vector[4000]
sigma <- df_draws_1$sigma # vector[4000]
y_pp_matriz[, j] <- rnorm(n_muestras, mu, sigma) # vector[4000]
}
df_pp_95_ci <- apply(y_pp_matriz, 2, quantile, probs = c(0.025, 0.975)) |>
t()|>
as.data.frame() |>
mutate(temp9am = temp9am_seq) |>
rename(li = `2.5%` , ls = `97.5%`)ggplot(df) +
geom_ribbon(
aes(x = temp9am, ymin = li, ymax = ls),
alpha = 0.3,
data = df_pp_95_ci
) +
geom_abline(
aes(intercept = beta0, slope = beta1),
alpha = 0.3,
color = "gray30",
data = df_draws_1[sample(4000, 40), ]
) +
geom_point(aes(x = temp9am, y = temp3pm, color = location), alpha = 0.7, size = 2) +
scale_color_manual(values = c(c_orange_dark, c_green_blue)) +
labs(
x = "Temperatura a las 9 a.m. (C°)",
y = "Temperatura a las 3 p.m. (C°)",
color = "Ciudad"
) +
theme_bw()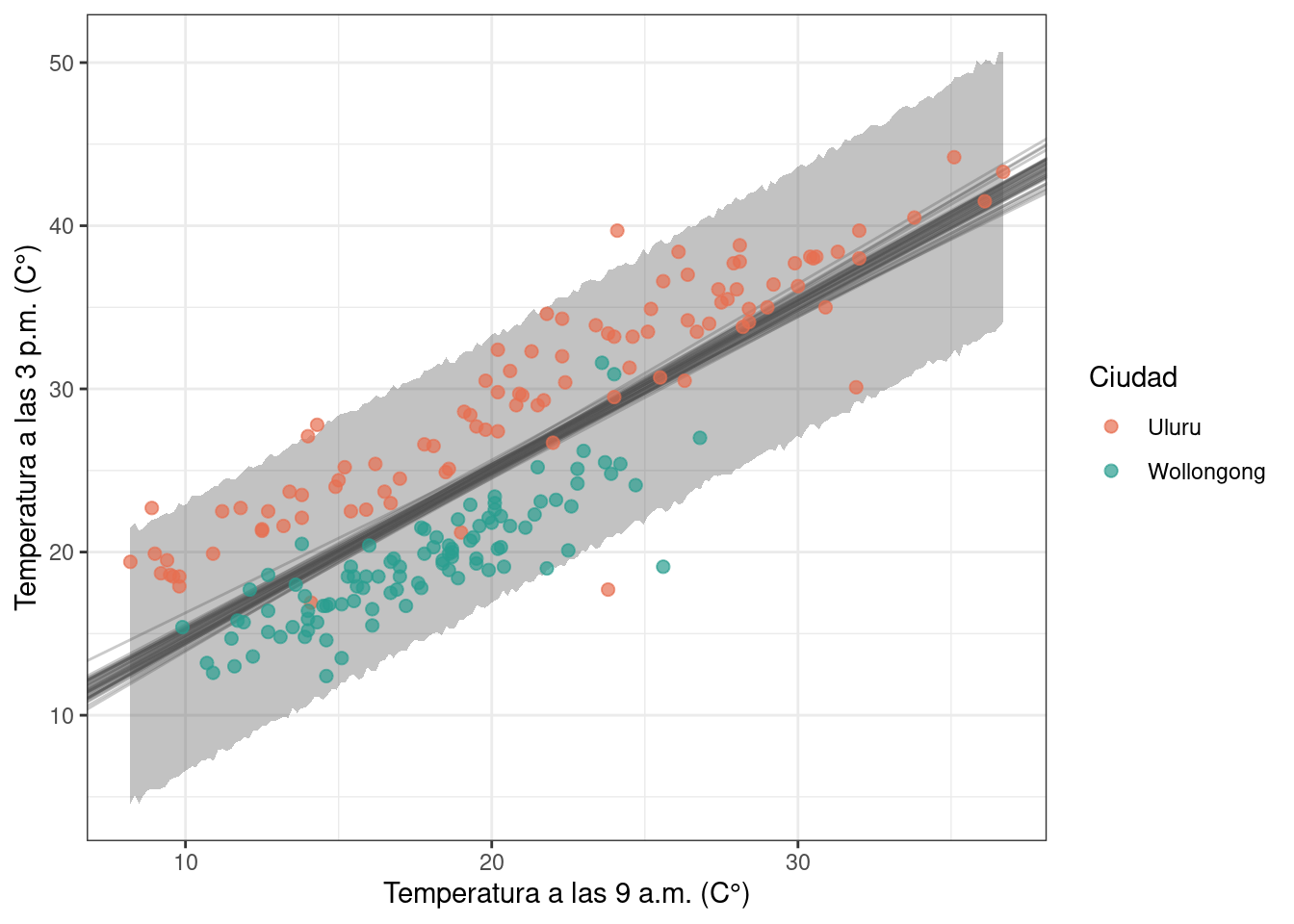
Modelo 2
stan/australia/modelo_2.stan
data {
int<lower=0> N; // Cantidad de observaciones
array[N] int location_idx; // Índice de la ciudad
vector[N] temp3pm; // Temperatura a las 3 pm (respuesta)
}
parameters {
vector[2] beta0; // Interceptos
real<lower=0> sigma; // Desvío estándar del error
}
transformed parameters {
vector[N] mu; // Predictor lineal
mu = beta0[location_idx];
}
model {
beta0 ~ normal(17.5, 6.25);
sigma ~ normal(0, 15);
temp3pm ~ normal(mu, sigma);
}
generated quantities {
vector[N] y_rep;
vector[N] log_likelihood;
for (i in 1:N) {
// Obtención de muestras de la distribución predictiva a posteriori
y_rep[i] = normal_rng(mu[i], sigma);
// Cálculo de la log-verosimilitud
log_likelihood[i] = normal_lpdf(temp3pm[i] | mu[i], sigma);
}
}Este modelo incorpora la ubicación. Una forma de implementarlo es utilizando índices que indiquen a que ubicación pertence cada observación.
as.factor(df$location) [1] Uluru Uluru Uluru Uluru Uluru Uluru
[7] Uluru Uluru Uluru Uluru Uluru Uluru
[13] Uluru Uluru Uluru Uluru Uluru Uluru
[19] Uluru Uluru Uluru Uluru Uluru Uluru
[25] Uluru Uluru Uluru Uluru Uluru Uluru
[31] Uluru Uluru Uluru Uluru Uluru Uluru
[37] Uluru Uluru Uluru Uluru Uluru Uluru
[43] Uluru Uluru Uluru Uluru Uluru Uluru
[49] Uluru Uluru Uluru Uluru Uluru Uluru
[55] Uluru Uluru Uluru Uluru Uluru Uluru
[61] Uluru Uluru Uluru Uluru Uluru Uluru
[67] Uluru Uluru Uluru Uluru Uluru Uluru
[73] Uluru Uluru Uluru Uluru Uluru Uluru
[79] Uluru Uluru Uluru Uluru Uluru Uluru
[85] Uluru Uluru Uluru Uluru Uluru Uluru
[91] Uluru Uluru Uluru Uluru Uluru Uluru
[97] Uluru Uluru Uluru Uluru Wollongong Wollongong
[103] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[109] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[115] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[121] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[127] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[133] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[139] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[145] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[151] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[157] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[163] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[169] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[175] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[181] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[187] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[193] Wollongong Wollongong Wollongong Wollongong Wollongong Wollongong
[199] Wollongong Wollongong
Levels: Uluru Wollongongas.integer(as.factor(df$location)) [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[38] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
[112] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[149] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[186] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2stan_data_2 <- list(
N = nrow(df),
location_idx = as.integer(as.factor(df$location)),
temp3pm = df$temp3pm
)
ruta_modelo_2 <- here::here(
"recursos", "codigo", "stan", "australia", "modelo_2.stan"
)
modelo_2 <- stan_model(file = ruta_modelo_2)
modelo_2_fit <- sampling(
modelo_2,
data = stan_data_2,
chains = 4,
seed = 1211,
refresh = 0,
)
# Extraemos las muestras del posterior y renombramos la columnas de beta0
df_draws_2 <- as.data.frame(extract(modelo_2_fit, c("beta0", "sigma")))
colnames(df_draws_2) <- c("beta0[Uluru]", "beta0[Wollongong]", "sigma")El código para visualizar los posteriors marginales es análogo.
df_draws_long_2 <- df_draws_2 |>
tidyr::pivot_longer(
c("beta0[Uluru]", "beta0[Wollongong]", "sigma"),
names_to = "parametro"
)
ggplot(df_draws_long_2) +
geom_histogram(
aes(x = value, y = after_stat(density)),
bins = 30,
fill = c_orange_light,
color = c_orange_light
) +
facet_wrap(~ parametro, scales = "free") +
labs(x = "Valor", y = "Densidad") +
theme_bw()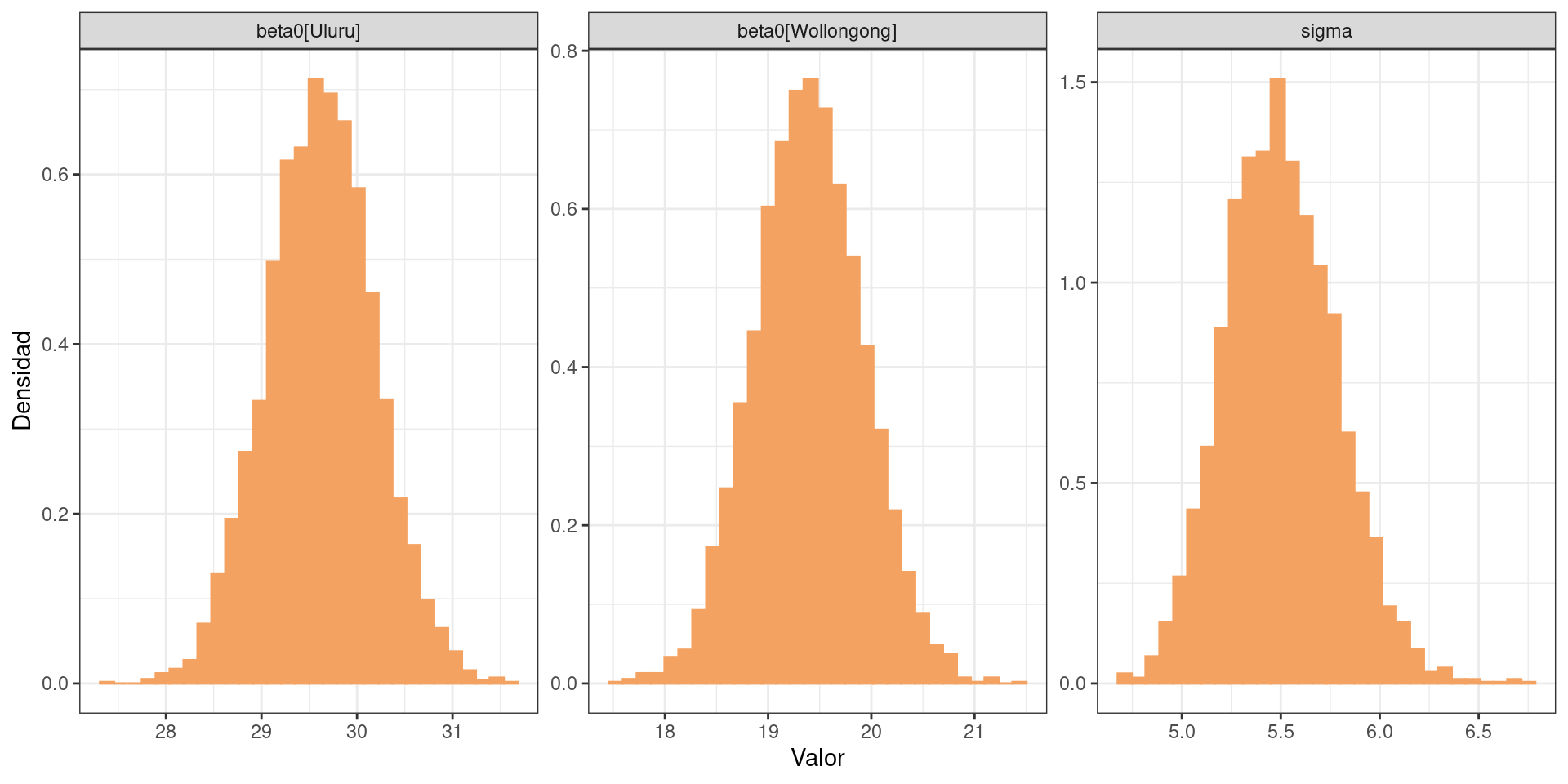
En este segundo modelo se tienen dos interceptos, uno para cada ciudad, y una pendiente nula.
data_lines <- data.frame(
beta0 = c(df_draws_2[["beta0[Uluru]"]], df_draws_2[["beta0[Wollongong]"]]),
location = rep(c("Uluru", "Wollongong"), each = nrow(df_draws_2))
)
ggplot(df) +
geom_point(aes(x = temp9am, y = temp3pm, color = location), alpha = 0.7, size = 2) +
geom_abline(
aes(intercept = beta0, slope = 0, color = location),
alpha = 0.3,
data = data_lines[sample(nrow(data_lines), 80), ]
) +
scale_color_manual(values = c(c_orange_dark, c_green_blue)) +
labs(
x = "Temperatura a las 9 a.m. (C°)",
y = "Temperatura a las 3 p.m. (C°)",
color = "Ciudad"
) +
theme_bw()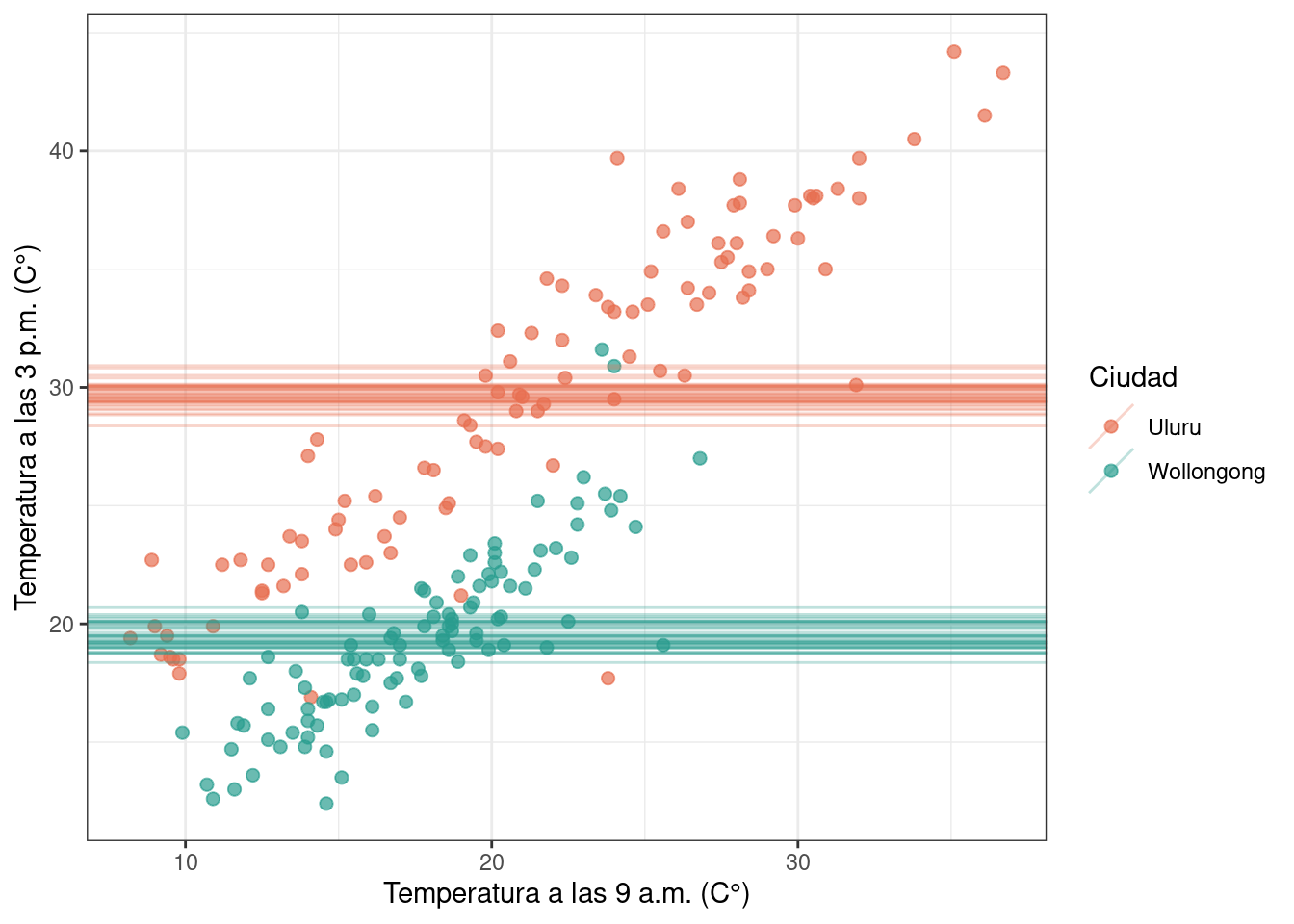
El modelo predice una temperatura única para cada ciudad a las 3 p.m., independiente de la temperatura a las 9 a.m.
La banda de credibilidad para las predicciones se obtiene y visualiza debajo.
n_muestras <- 4000
n_grilla <- 200
temp9am_seq <- seq(min(df$temp9am), max(df$temp9am), length.out = n_grilla)
y_pp_matriz_u <- matrix(nrow = n_muestras, ncol = n_grilla)
y_pp_matriz_w <- matrix(nrow = n_muestras, ncol = n_grilla)
for (j in seq_len(n_grilla)) {
mu_u <- df_draws_2[["beta0[Uluru]"]] # vector[4000]
mu_w <- df_draws_2[["beta0[Wollongong]"]] # vector[4000]
sigma <- df_draws_2$sigma # vector[4000]
y_pp_matriz_u[, j] <- rnorm(n_muestras, mu_u, sigma) # vector[4000]
y_pp_matriz_w[, j] <- rnorm(n_muestras, mu_w, sigma) # vector[4000]
}
df_pp_95_ci_u <- apply(y_pp_matriz_u, 2, quantile, probs = c(0.025, 0.975)) |>
t()|>
as.data.frame() |>
mutate(temp9am = temp9am_seq) |>
rename(li = `2.5%` , ls = `97.5%`)
df_pp_95_ci_w <- apply(y_pp_matriz_w, 2, quantile, probs = c(0.025, 0.975)) |>
t()|>
as.data.frame() |>
mutate(temp9am = temp9am_seq) |>
rename(li = `2.5%` , ls = `97.5%`)ggplot(df) +
geom_ribbon(
aes(x = temp9am, ymin = li, ymax = ls),
alpha = 0.3,
data = df_pp_95_ci_u,
fill = c_orange_dark
) +
geom_ribbon(
aes(x = temp9am, ymin = li, ymax = ls),
alpha = 0.3,
data = df_pp_95_ci_w,
fill = c_green_blue
) +
geom_abline(
aes(intercept = beta0, slope = 0, color = location),
alpha = 0.3,
data = data_lines[sample(nrow(data_lines), 80), ]
) +
geom_point(aes(x = temp9am, y = temp3pm, color = location), alpha = 0.7, size = 2) +
scale_color_manual(values = c(c_orange_dark, c_green_blue)) +
labs(
x = "Temperatura a las 9 a.m. (C°)",
y = "Temperatura a las 3 p.m. (C°)",
color = "Ciudad"
) +
theme_bw()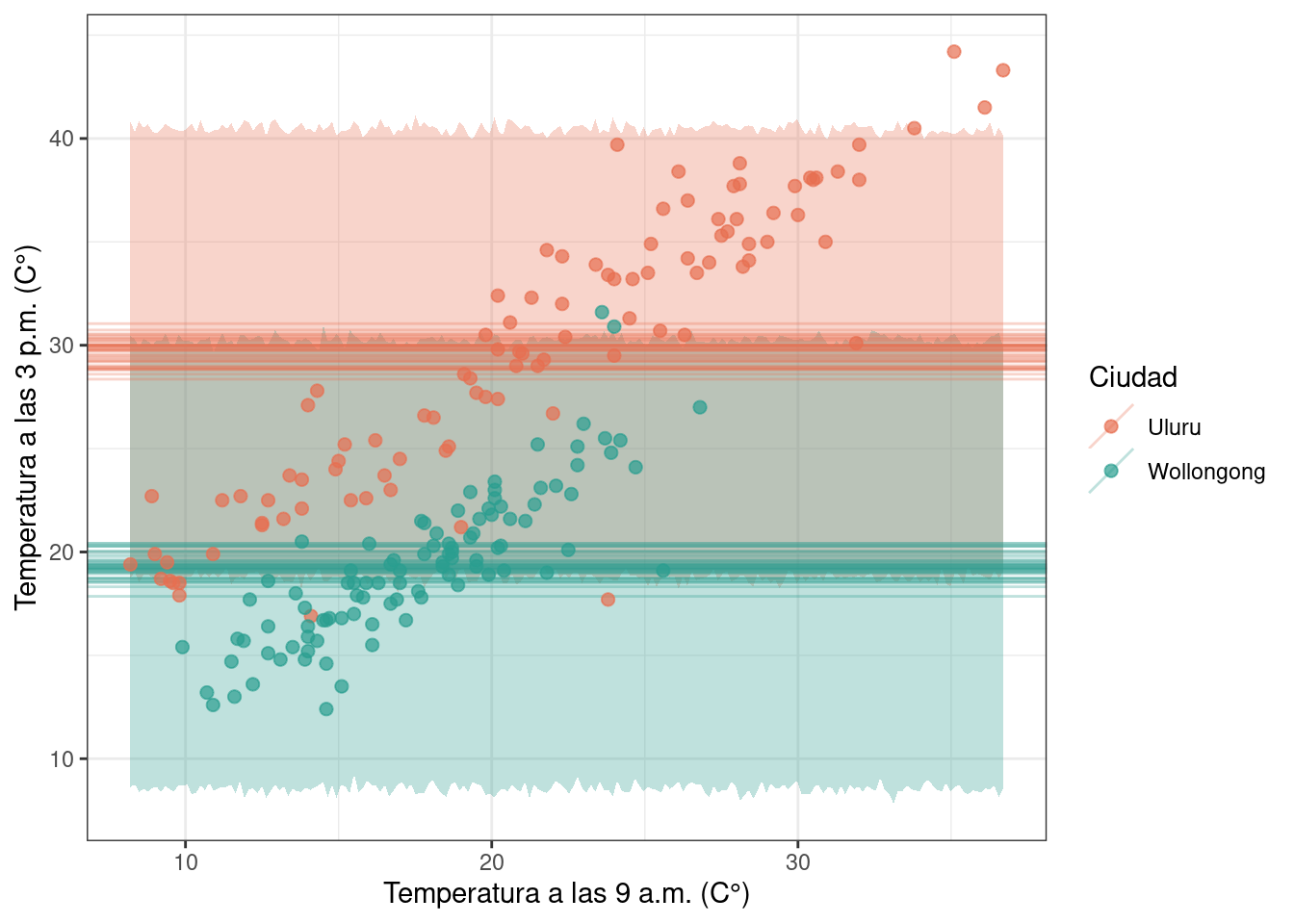
Modelo 3
stan/australia/modelo_3.stan
data {
int<lower=0> N; // Cantidad de observaciones
array[N] int location_idx; // Índice de la ciudad
vector[N] temp9am; // Temperatura a las 9 am (predictor)
vector[N] temp3pm; // Temperatura a las 3 pm (respuesta)
}
parameters {
vector[2] beta0; // Interceptos
real beta1; // Pendiente
real<lower=0> sigma; // Desvío estándar del error
}
transformed parameters {
vector[N] mu; // Predictor lineal
mu = beta0[location_idx] + beta1 * temp9am;
}
model {
beta0 ~ normal(17.5, 6.25);
beta1 ~ normal(0, 10);
sigma ~ normal(0, 15);
temp3pm ~ normal(mu, sigma);
}
generated quantities {
vector[N] y_rep;
vector[N] log_likelihood;
for (i in 1:N) {
// Obtención de muestras de la distribución predictiva a posteriori
y_rep[i] = normal_rng(mu[i], sigma);
// Cálculo de la log-verosimilitud
log_likelihood[i] = normal_lpdf(temp3pm[i] | mu[i], sigma);
}
}Este último modelo presenta un intercepto distinto para cada ciudad y una pendiente común a ambas. Por lo tanto, es necesario pasarle a Stan el vector de índices para las ciudades y la temperatura a las 9 a.m.
stan_data_3 <- list(
N = nrow(df),
location_idx = as.integer(as.factor(df$location)),
temp9am = df$temp9am,
temp3pm = df$temp3pm
)
ruta_modelo_3 <- here::here(
"recursos", "codigo", "stan", "australia", "modelo_3.stan"
)
modelo_3 <- stan_model(file = ruta_modelo_3)
modelo_3_fit <- sampling(
modelo_3,
data = stan_data_3,
chains = 4,
refresh = 0,
seed = 1211
)
df_draws_3 <- as.data.frame(extract(modelo_3_fit, c("beta0", "beta1", "sigma")))
colnames(df_draws_3) <- c("beta0[Uluru]", "beta0[Wollongong]", "beta1", "sigma")df_draws_long_3 <- df_draws_3 |>
tidyr::pivot_longer(
c("beta0[Uluru]", "beta0[Wollongong]", "beta1", "sigma"),
names_to = "parametro"
)
ggplot(df_draws_long_3) +
geom_histogram(
aes(x = value, y = after_stat(density)),
bins = 30,
fill = c_orange_light,
color = c_orange_light
) +
facet_wrap(~ parametro, scales = "free") +
labs(x = "Valor", y = "Densidad") +
theme_bw()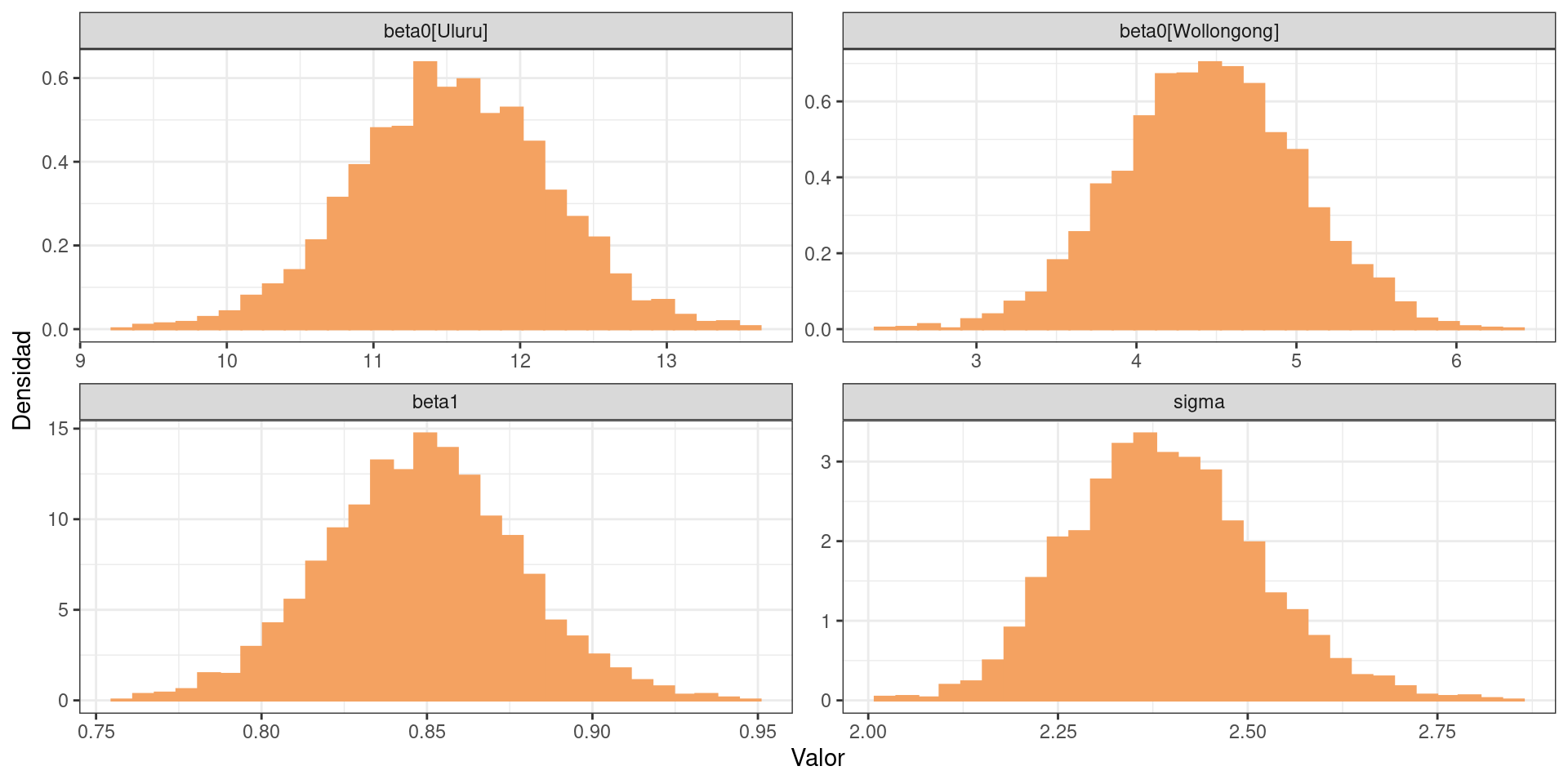
data_lines <- data.frame(
beta0 = c(df_draws_3[["beta0[Uluru]"]], df_draws_3[["beta0[Wollongong]"]]),
beta1 = rep(df_draws_3[["beta1"]], 2),
location = rep(c("Uluru", "Wollongong"), each = nrow(df_draws_3))
)
ggplot(df) +
geom_abline(
aes(intercept = beta0, slope = beta1, color = location),
alpha = 0.3,
data = data_lines[sample(nrow(data_lines), 80), ]
) +
geom_point(aes(x = temp9am, y = temp3pm, color = location), alpha = 0.7, size = 2) +
scale_color_manual(values = c(c_orange_dark, c_green_blue)) +
labs(
x = "Temperatura a las 9 a.m. (C°)",
y = "Temperatura a las 3 p.m. (C°)",
color = "Ciudad"
) +
theme_bw()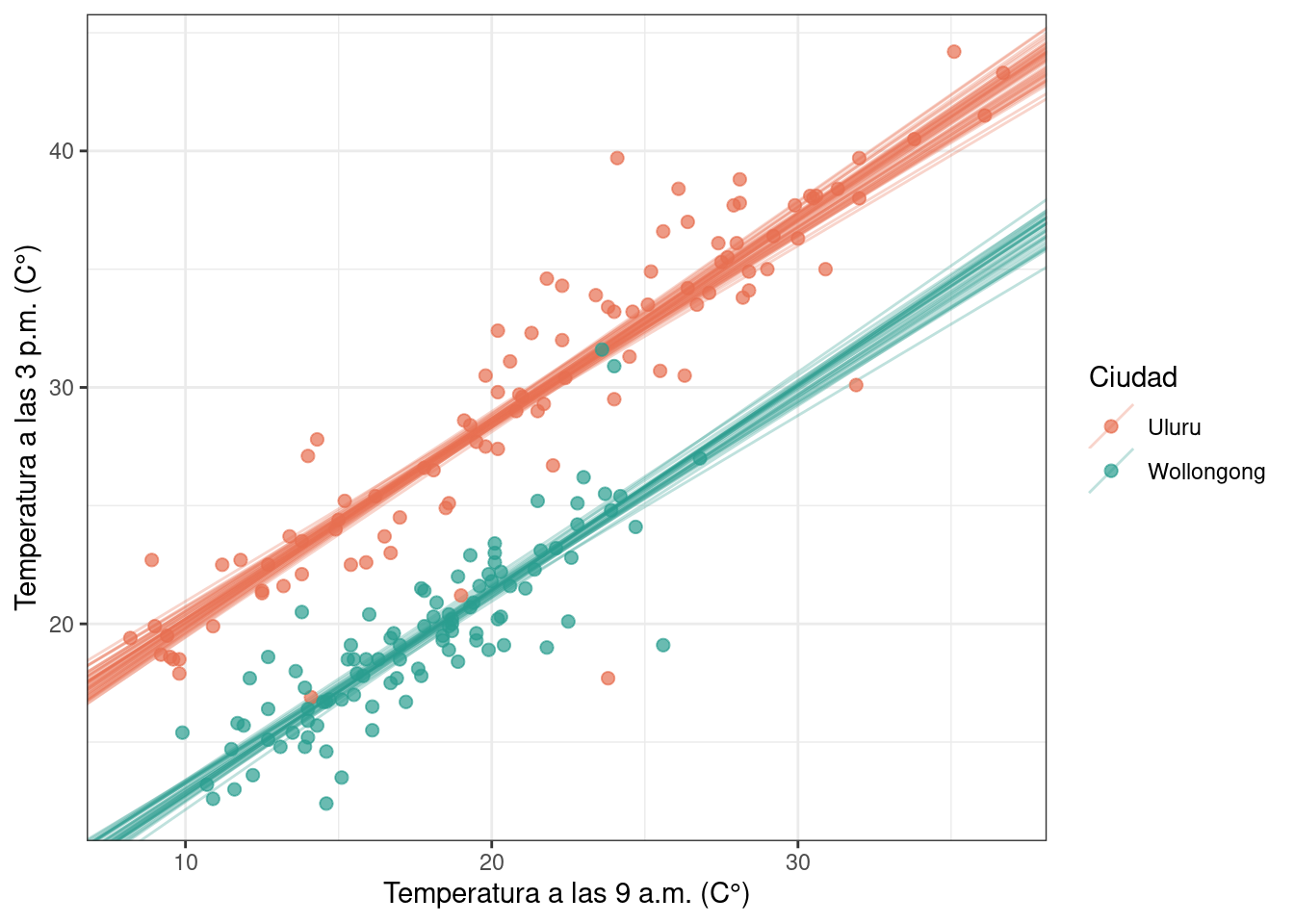
De manera cualitativa, es posible ver que este modelo ajusta a la nube de puntos mejor que los anteriores.
Código
n_muestras <- 4000
n_grilla <- 200
temp9am_seq <- seq(min(df$temp9am), max(df$temp9am), length.out = n_grilla)
y_pp_matriz_u <- matrix(nrow = n_muestras, ncol = n_grilla)
y_pp_matriz_w <- matrix(nrow = n_muestras, ncol = n_grilla)
for (j in seq_len(n_grilla)) {
mu_u <- df_draws_3[["beta0[Uluru]"]] + temp9am_seq[j] * df_draws_3[["beta1"]] # vector[4000]
mu_w <- df_draws_3[["beta0[Wollongong]"]] + temp9am_seq[j] * df_draws_3[["beta1"]] # vector[4000]
sigma <- df_draws_3$sigma # vector[4000]
y_pp_matriz_u[, j] <- rnorm(n_muestras, mu_u, sigma) # vector[4000]
y_pp_matriz_w[, j] <- rnorm(n_muestras, mu_w, sigma) # vector[4000]
}
df_pp_95_ci_u <- apply(y_pp_matriz_u, 2, quantile, probs = c(0.025, 0.975)) |>
t()|>
as.data.frame() |>
mutate(temp9am = temp9am_seq) |>
rename(li = `2.5%` , ls = `97.5%`)
df_pp_95_ci_w <- apply(y_pp_matriz_w, 2, quantile, probs = c(0.025, 0.975)) |>
t()|>
as.data.frame() |>
mutate(temp9am = temp9am_seq) |>
rename(li = `2.5%` , ls = `97.5%`)Código
ggplot(df) +
geom_ribbon(
aes(x = temp9am, ymin = li, ymax = ls),
alpha = 0.3,
data = df_pp_95_ci_u,
fill = c_orange_dark
) +
geom_ribbon(
aes(x = temp9am, ymin = li, ymax = ls),
alpha = 0.3,
data = df_pp_95_ci_w,
fill = c_green_blue
) +
geom_abline(
aes(intercept = beta0, slope = beta1, color = location),
alpha = 0.3,
data = data_lines[sample(nrow(data_lines), 80), ]
) +
geom_point(aes(x = temp9am, y = temp3pm, color = location), alpha = 0.7, size = 2) +
scale_color_manual(values = c(c_orange_dark, c_green_blue)) +
labs(
x = "Temperatura a las 9 a.m. (C°)",
y = "Temperatura a las 3 p.m. (C°)",
color = "Ciudad"
) +
theme_bw()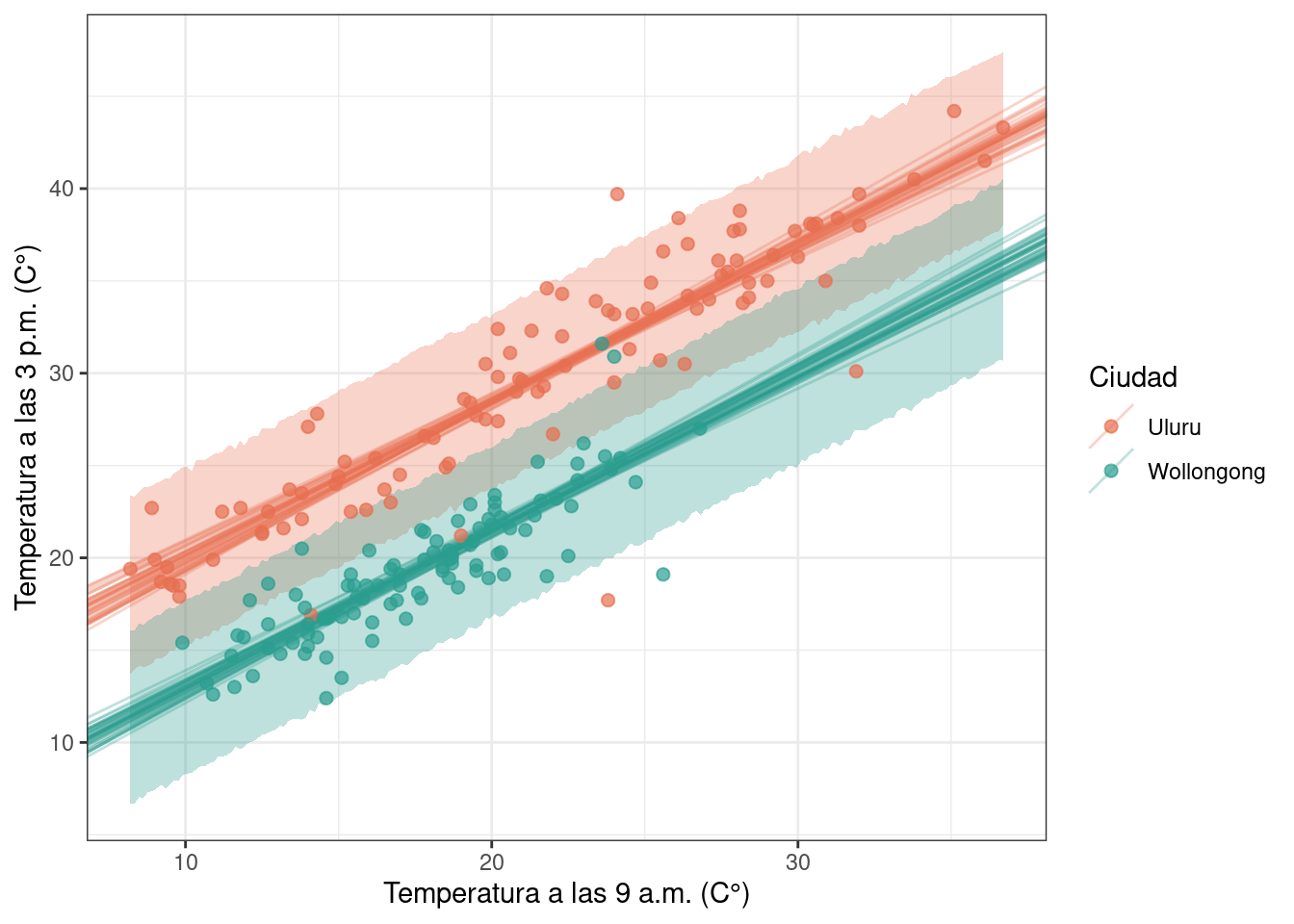
Modelo 4
Finalmente, un modelo que considera interceptos y pendientes específicas para cada ciudad.
stan/australia/modelo_4.stan
data {
int<lower=0> N; // Cantidad de observaciones
array[N] int location_idx; // Índice de la ciudad
vector[N] temp9am; // Temperatura a las 9 am (predictor)
vector[N] temp3pm; // Temperatura a las 3 pm (respuesta)
}
parameters {
vector[2] beta0; // Interceptos
vector[2] beta1; // Pendientes
real<lower=0> sigma; // Desvío estándar del error
}
transformed parameters {
vector[N] mu; // Predictor lineal
mu = beta0[location_idx] + beta1[location_idx] .* temp9am;
}
model {
beta0 ~ normal(17.5, 6.25);
beta1 ~ normal(0, 10);
sigma ~ normal(0, 15);
temp3pm ~ normal(mu, sigma);
}
generated quantities {
vector[N] y_rep;
vector[N] log_likelihood;
for (i in 1:N) {
// Obtención de muestras de la distribución predictiva a posteriori
y_rep[i] = normal_rng(mu[i], sigma);
// Cálculo de la log-verosimilitud
log_likelihood[i] = normal_lpdf(temp3pm[i] | mu[i], sigma);
}
}stan_data_4 <- list(
N = nrow(df),
location_idx = as.integer(as.factor(df$location)),
temp9am = df$temp9am,
temp3pm = df$temp3pm
)
ruta_modelo_4 <- here::here(
"recursos", "codigo", "stan", "australia", "modelo_4.stan"
)
modelo_4 <- stan_model(file = ruta_modelo_4)
modelo_4_fit <- sampling(
modelo_4,
data = stan_data_4,
chains = 4,
refresh = 0,
seed = 1211
)
df_draws_4 <- as.data.frame(extract(modelo_4_fit, c("beta0", "beta1", "sigma")))
colnames(df_draws_4) <- c(
"beta0[Uluru]", "beta0[Wollongong]", "beta1[Uluru]", "beta1[Wollongong]", "sigma"
)df_draws_long_4 <- df_draws_4 |>
tidyr::pivot_longer(
c("beta0[Uluru]", "beta0[Wollongong]", "beta1[Uluru]", "beta1[Wollongong]", "sigma"),
names_to = "parametro"
)
ggplot(df_draws_long_4) +
geom_histogram(
aes(x = value, y = after_stat(density)),
bins = 30,
fill = c_orange_light,
color = c_orange_light
) +
facet_wrap(~ parametro, scales = "free") +
labs(x = "Valor", y = "Densidad") +
theme_bw()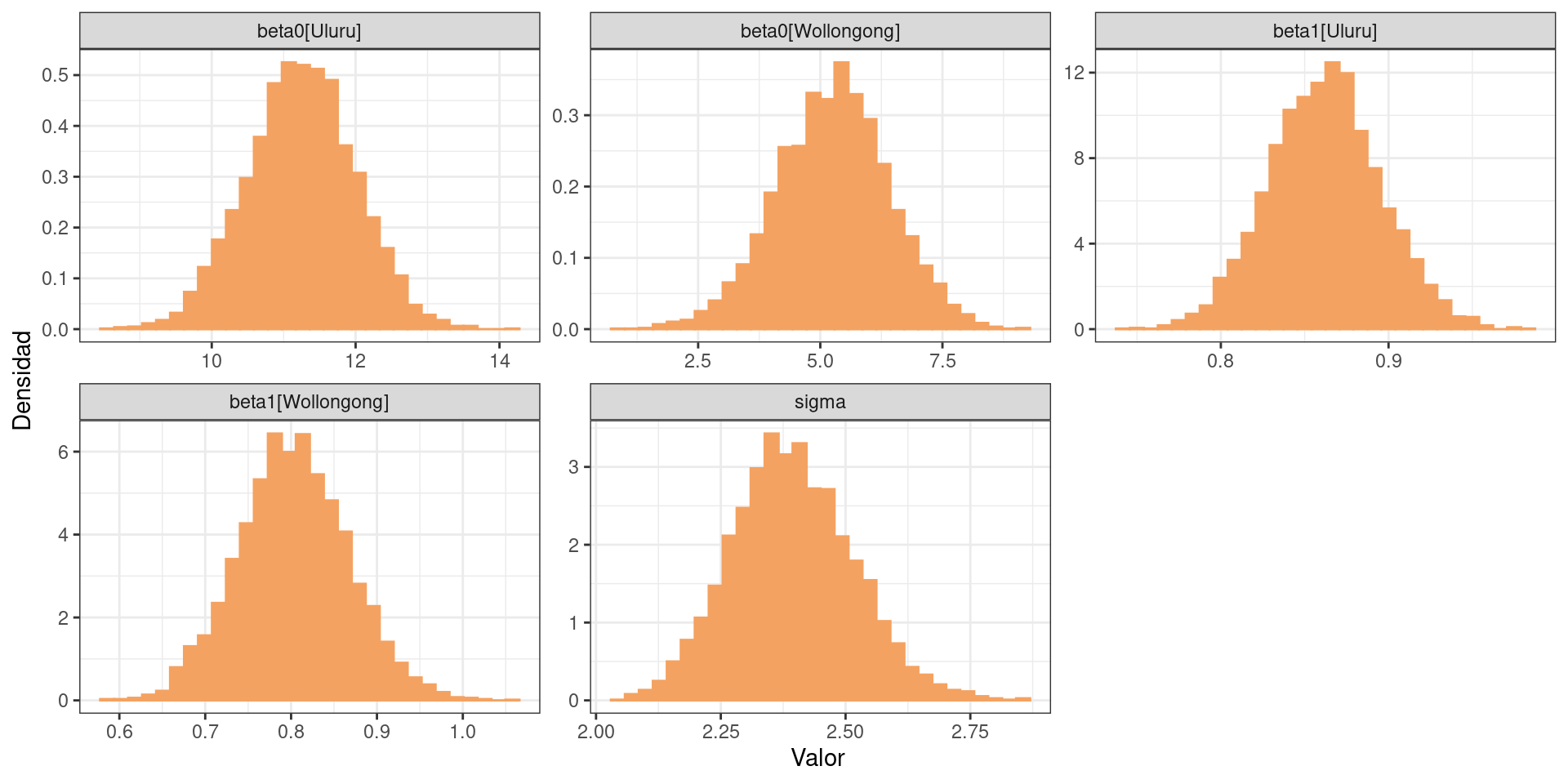
data_lines <- data.frame(
beta0 = c(df_draws_4[["beta0[Uluru]"]], df_draws_4[["beta0[Wollongong]"]]),
beta1 = c(df_draws_4[["beta1[Uluru]"]], df_draws_4[["beta1[Wollongong]"]]),
location = rep(c("Uluru", "Wollongong"), each = nrow(df_draws_4))
)
ggplot(df) +
geom_abline(
aes(intercept = beta0, slope = beta1, color = location),
alpha = 0.3,
data = data_lines[sample(nrow(data_lines), 80), ]
) +
geom_point(aes(x = temp9am, y = temp3pm, color = location), alpha = 0.7, size = 2) +
scale_color_manual(values = c(c_orange_dark, c_green_blue)) +
labs(
x = "Temperatura a las 9 a.m. (C°)",
y = "Temperatura a las 3 p.m. (C°)",
color = "Ciudad"
) +
theme_bw()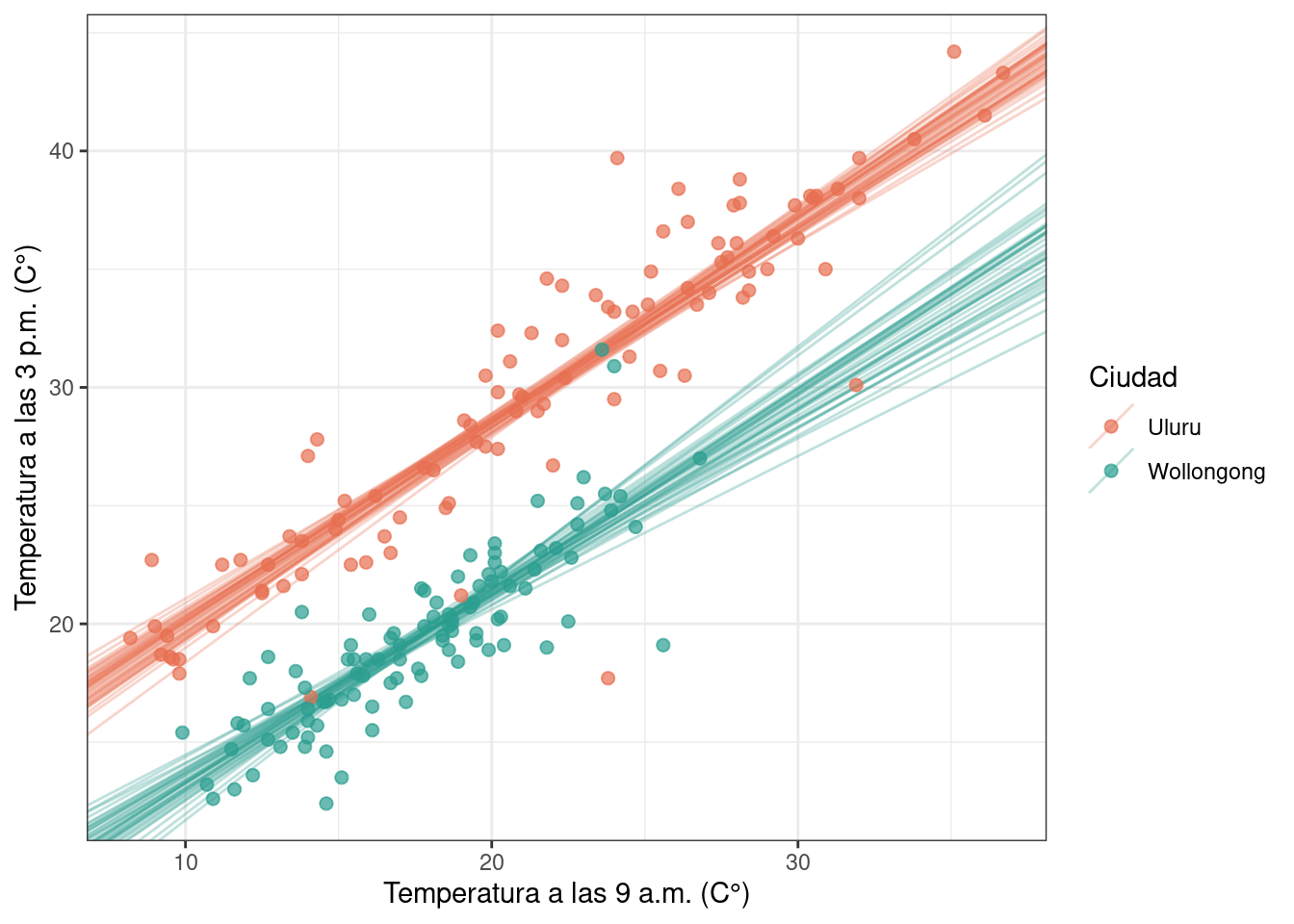
Código
n_muestras <- 4000
n_grilla <- 200
temp9am_seq <- seq(min(df$temp9am), max(df$temp9am), length.out = n_grilla)
y_pp_matriz_u <- matrix(nrow = n_muestras, ncol = n_grilla)
y_pp_matriz_w <- matrix(nrow = n_muestras, ncol = n_grilla)
for (j in seq_len(n_grilla)) {
mu_u <- df_draws_4[["beta0[Uluru]"]] + temp9am_seq[j] * df_draws_4[["beta1[Uluru]"]]
mu_w <- df_draws_4[["beta0[Wollongong]"]] + temp9am_seq[j] * df_draws_4[["beta1[Uluru]"]]
sigma <- df_draws_4$sigma
y_pp_matriz_u[, j] <- rnorm(n_muestras, mu_u, sigma)
y_pp_matriz_w[, j] <- rnorm(n_muestras, mu_w, sigma)
}
df_pp_95_ci_u <- apply(y_pp_matriz_u, 2, quantile, probs = c(0.025, 0.975)) |>
t()|>
as.data.frame() |>
mutate(temp9am = temp9am_seq) |>
rename(li = `2.5%` , ls = `97.5%`)
df_pp_95_ci_w <- apply(y_pp_matriz_w, 2, quantile, probs = c(0.025, 0.975)) |>
t()|>
as.data.frame() |>
mutate(temp9am = temp9am_seq) |>
rename(li = `2.5%` , ls = `97.5%`)Código
ggplot(df) +
geom_ribbon(
aes(x = temp9am, ymin = li, ymax = ls),
alpha = 0.3,
data = df_pp_95_ci_u,
fill = c_orange_dark
) +
geom_ribbon(
aes(x = temp9am, ymin = li, ymax = ls),
alpha = 0.3,
data = df_pp_95_ci_w,
fill = c_green_blue
) +
geom_abline(
aes(intercept = beta0, slope = beta1, color = location),
alpha = 0.3,
data = data_lines[sample(nrow(data_lines), 80), ]
) +
geom_point(aes(x = temp9am, y = temp3pm, color = location), alpha = 0.7, size = 2) +
scale_color_manual(values = c(c_orange_dark, c_green_blue)) +
labs(
x = "Temperatura a las 9 a.m. (C°)",
y = "Temperatura a las 3 p.m. (C°)",
color = "Ciudad"
) +
theme_bw()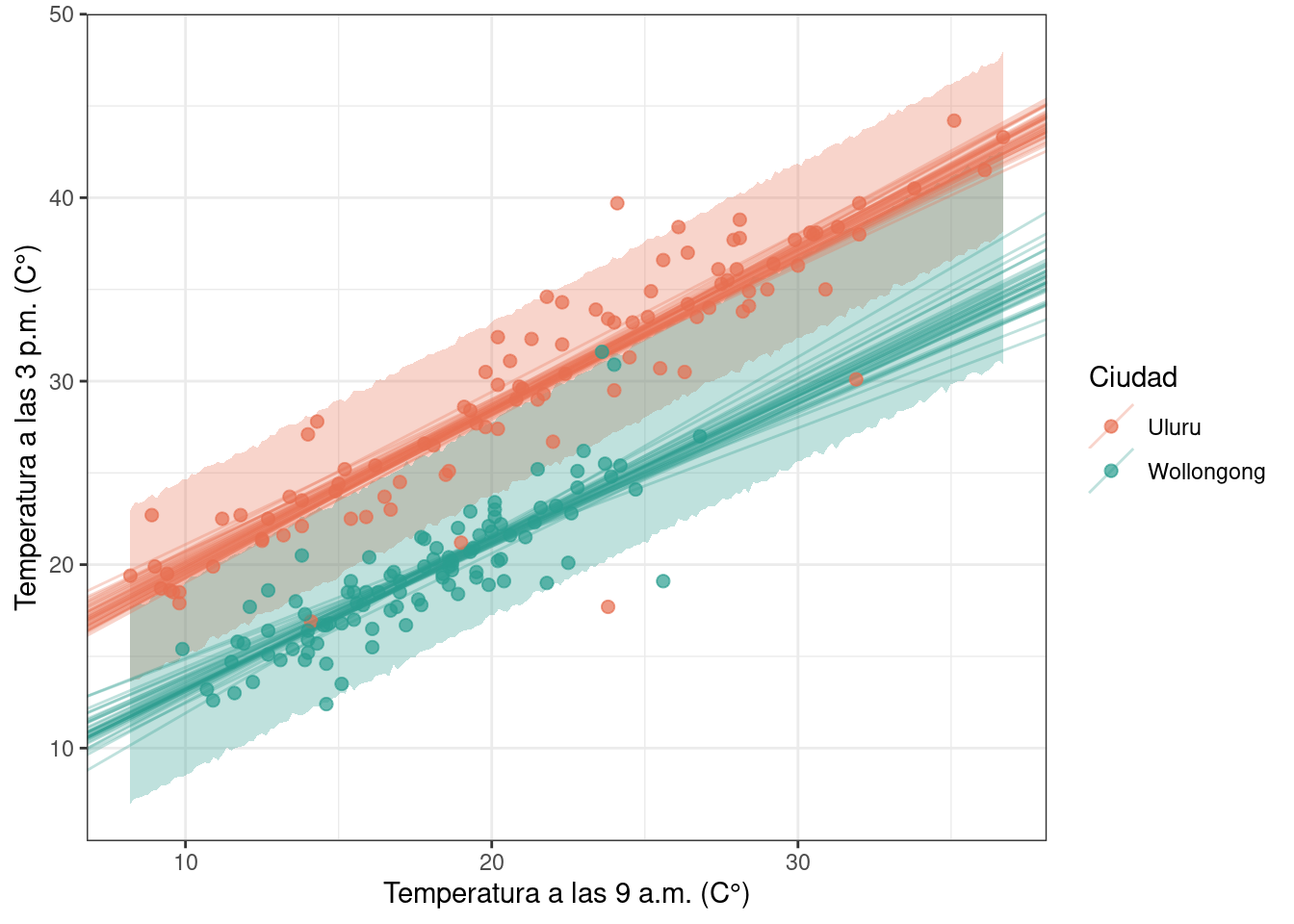
Con este modelo es posible también obtener y visualizar la distribución a posteriori de la diferencia entre pendientes.
df_draws_4 |>
mutate(pendiente_diff = `beta1[Uluru]` - `beta1[Wollongong]`) |>
ggplot() +
geom_histogram(
aes(x = pendiente_diff, y = after_stat(density)),
bins = 30,
fill = c_orange_light,
color = c_orange_light
) +
labs(x = expression(beta["1, U"] - beta["1, W"]), y = "Densidad") +
theme_bw()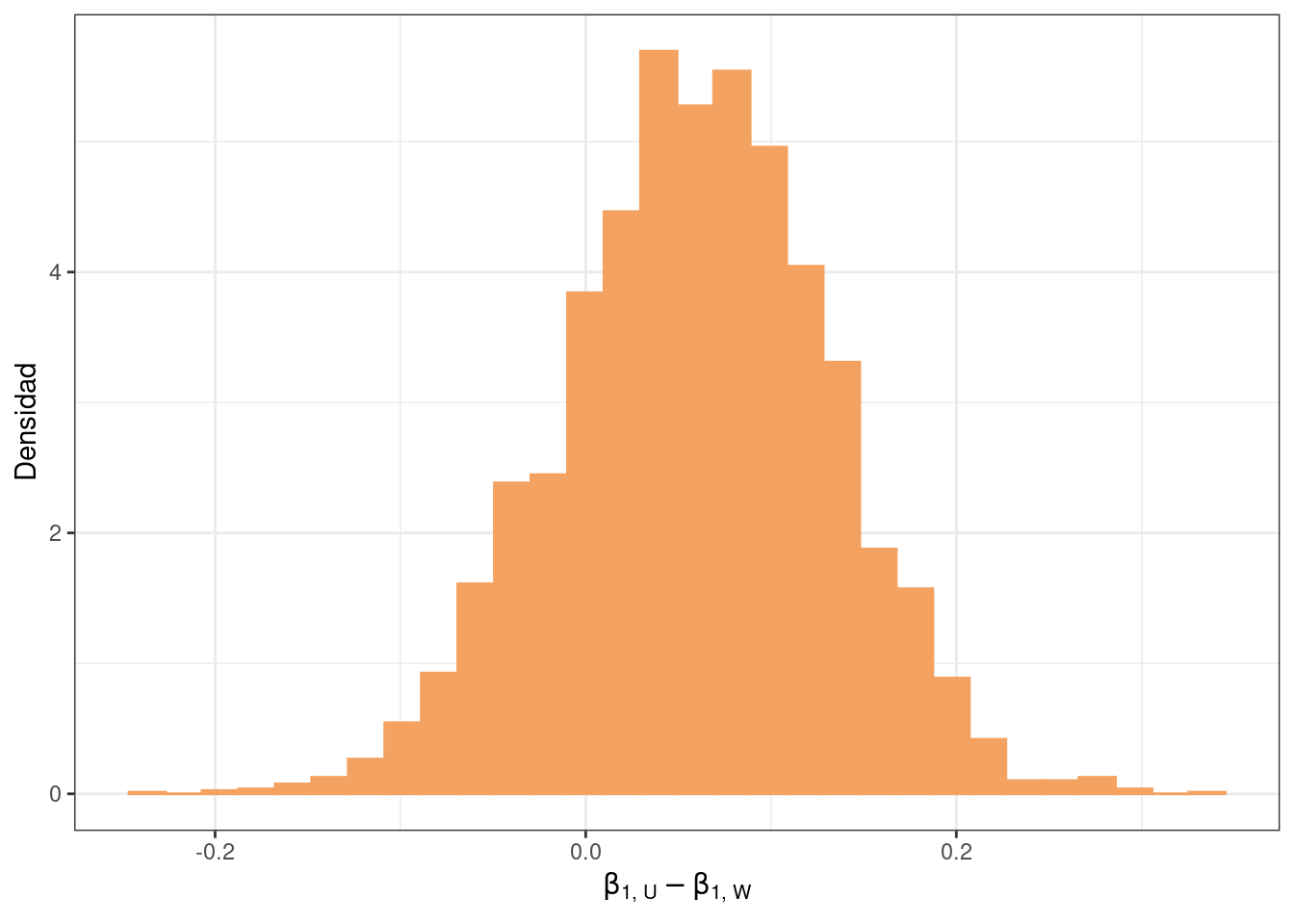
¿Qué indica el gráfico?
Antes de pasar a la comparación de modelos, podemos visualizar la distribución a posteriori marginal para \(\sigma\) en cada modelo (¿qué nos indica?):
df_sigmas <- data.frame(
sigma = c(df_draws_1$sigma, df_draws_2$sigma, df_draws_3$sigma, df_draws_4$sigma),
modelo = rep(c("Modelo 1", "Modelo 2", "Modelo 3", "Modelo 4"), each = 4000)
)
ggplot(df_sigmas) +
geom_histogram(
aes(x = sigma, y = after_stat(density)),
bins = 40,
fill = c_orange_light,
color = c_orange_light
) +
facet_wrap(~ modelo, scales = "free", nrow = 1) +
labs(x = expression(sigma), y = "Densidad") +
theme_bw()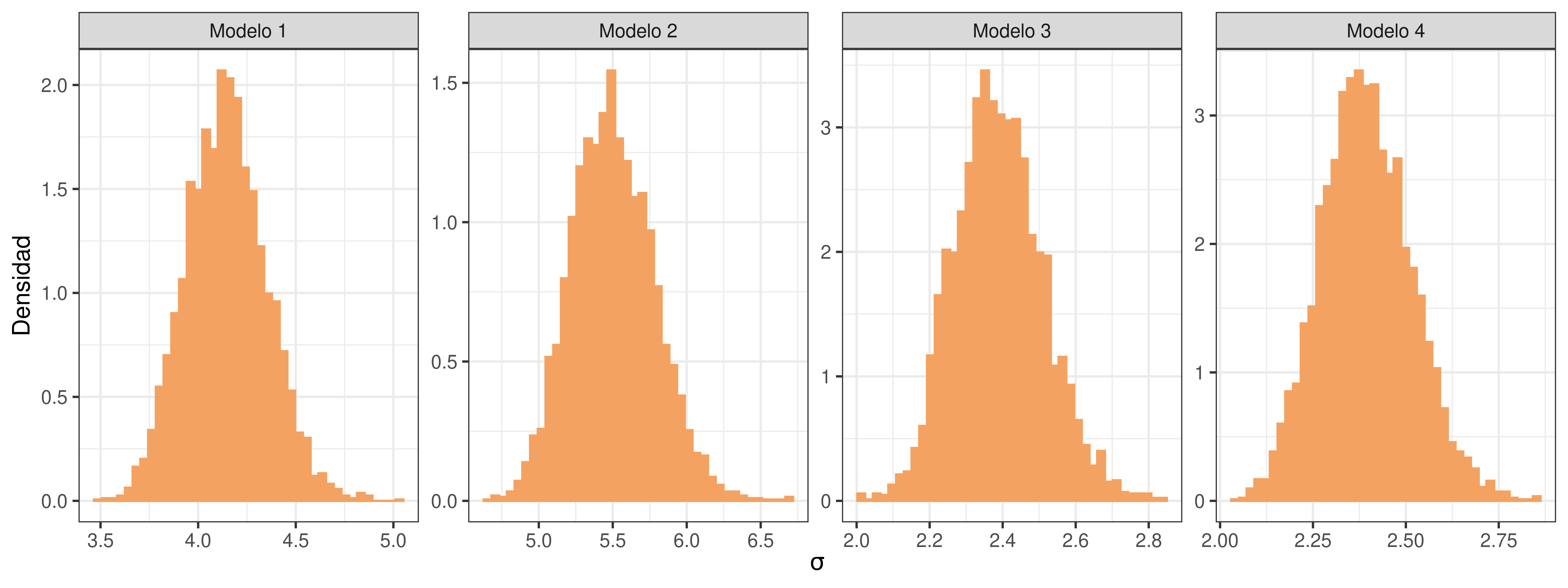
Comparación
Posterior predictive checks
La librería {bayesplot} nos permite realizar pruebas predictivas a posteriori mediante el uso de ppc_dens_overlay(). El gráfico que se obtiene permite comparar la distribución empírica de los datos (marginal) con distribuciones estimadas a partir de valores de la distribución predictiva a posteriori.
Para crear este gráfico es necesario haber obtenido muestras de la distribución predictiva a posteriori con Stan. En nuestro caso, las guardamos en y_rep.
library(bayesplot)
# Notar que solo se muestran 200 muestras para que el gráfico quede menos cargado.
y_rep_1 <- extract(modelo_1_fit, "y_rep")$y_rep
ppc_dens_overlay(df$temp3pm, y_rep_1[sample(2000, 200), ]) +
labs(x = "Temperatura a las 3 p.m. (C°)", y = "Densidad") +
theme_bw()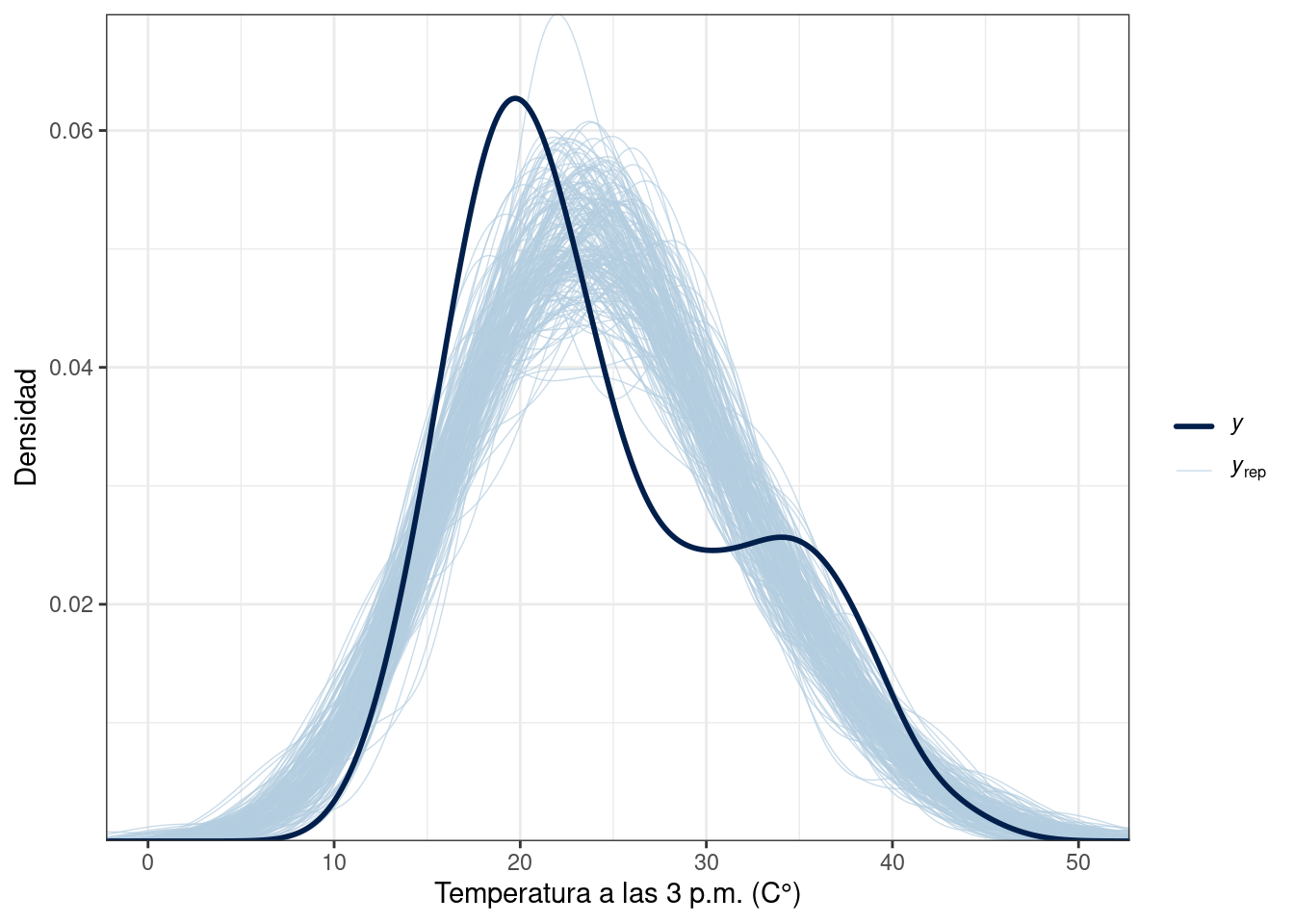
y_rep_2 <- extract(modelo_2_fit, "y_rep")$y_rep
ppc_dens_overlay(df$temp3pm, y_rep_2[sample(2000, 200), ]) +
labs(x = "Temperatura a las 3 p.m. (C°)", y = "Densidad") +
theme_bw()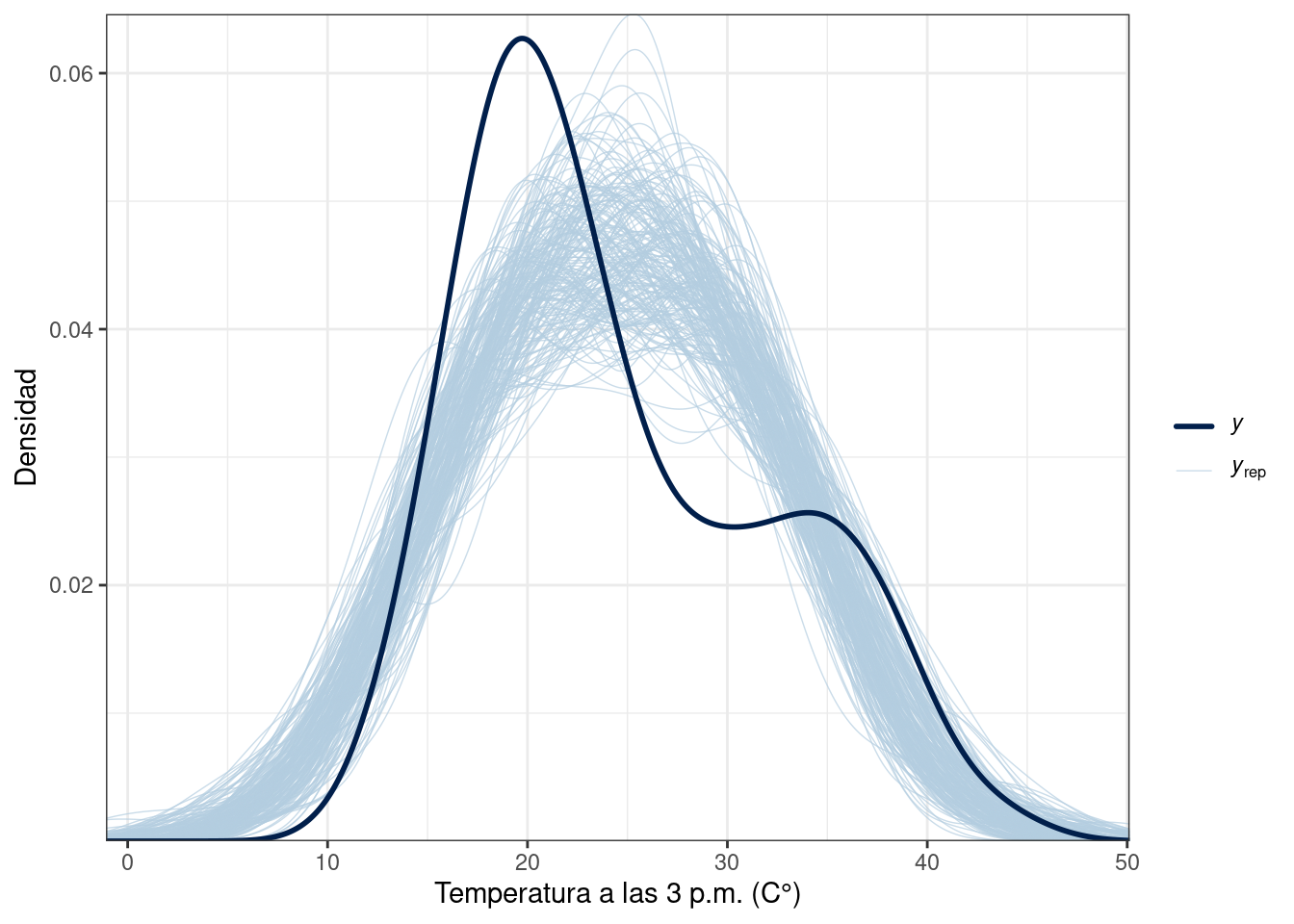
y_rep_3 <- extract(modelo_3_fit, "y_rep")$y_rep
ppc_dens_overlay(df$temp3pm, y_rep_3[sample(2000, 200), ]) +
labs(x = "Temperatura a las 3 p.m. (C°)", y = "Densidad") +
theme_bw()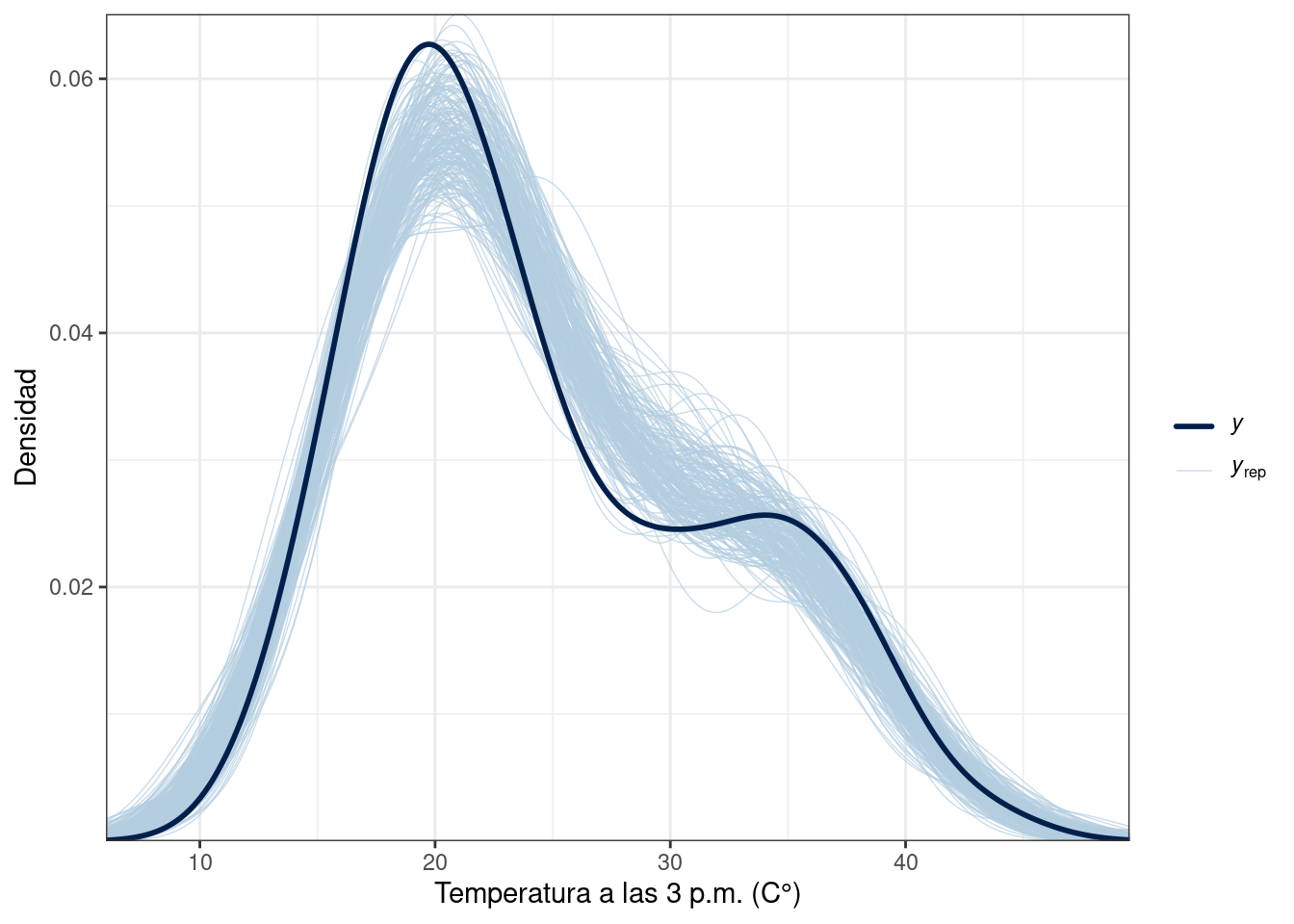
y_rep_4 <- extract(modelo_4_fit, "y_rep")$y_rep
ppc_dens_overlay(df$temp3pm, y_rep_3[sample(2000, 200), ]) +
labs(x = "Temperatura a las 3 p.m. (C°)", y = "Densidad") +
theme_bw()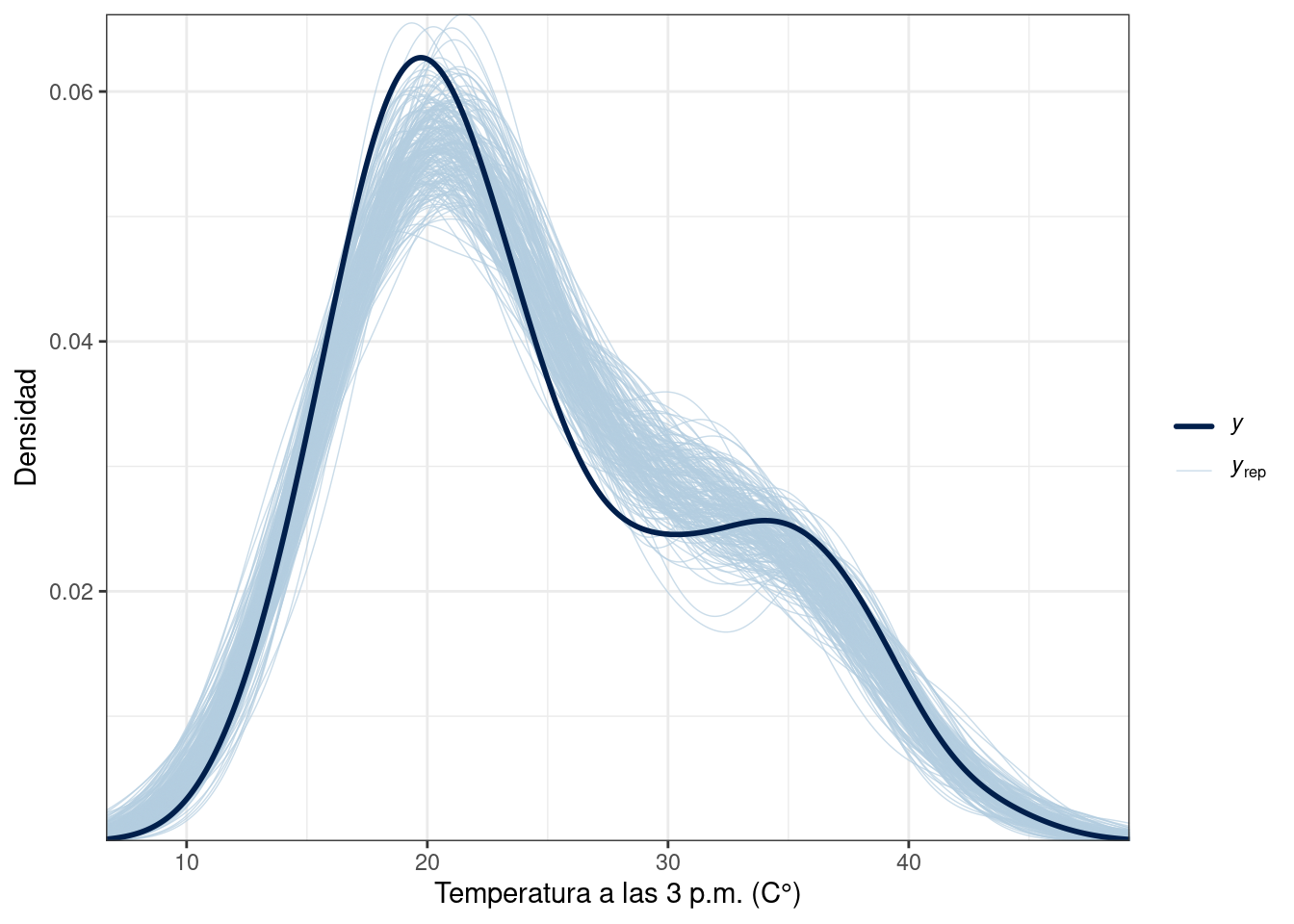
Las distribuciones generadas con los modelos 1 y 2 no replican fielmente la distribución empírica de la variable respuesta, mientras que las distribuciones generadas con el modelo 3 proveen una mejor aproximación.
LOO
En esta sección utilizamos la función loo() de la librería {loo} para estimar el ELPD (Expected log pointwise predictive density for a new dataset) mediante una aproximación a la validación cruzada conocido como PSIS-LOO CV.
Lo único que necesitamos es el objeto que obtuvimos al muestrear del posterior e indicar el nombre de la variable donde guardamos el cómputo del log-likelihood punto a punto (log_likelihood en todos los casos).
library(loo)
loo_1 <- loo(modelo_1_fit, pars = "log_likelihood")
loo_1
Computed from 4000 by 200 log-likelihood matrix.
Estimate SE
elpd_loo -568.4 8.4
p_loo 2.5 0.3
looic 1136.9 16.8
------
MCSE of elpd_loo is 0.0.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.3, 1.2]).
All Pareto k estimates are good (k < 0.7).
See help('pareto-k-diagnostic') for details.loo_2 <- loo(modelo_2_fit, pars = "log_likelihood")
loo_2
Computed from 4000 by 200 log-likelihood matrix.
Estimate SE
elpd_loo -625.7 9.5
p_loo 2.9 0.3
looic 1251.5 19.0
------
MCSE of elpd_loo is 0.0.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.9, 1.0]).
All Pareto k estimates are good (k < 0.7).
See help('pareto-k-diagnostic') for details.loo_3 <- loo(modelo_3_fit, pars = "log_likelihood")
loo_3
Computed from 4000 by 200 log-likelihood matrix.
Estimate SE
elpd_loo -461.1 22.8
p_loo 7.4 3.4
looic 922.1 45.7
------
MCSE of elpd_loo is NA.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.4, 1.2]).
Pareto k diagnostic values:
Count Pct. Min. ESS
(-Inf, 0.7] (good) 199 99.5% 928
(0.7, 1] (bad) 1 0.5% <NA>
(1, Inf) (very bad) 0 0.0% <NA>
See help('pareto-k-diagnostic') for details.loo_4 <- loo(modelo_4_fit, pars = "log_likelihood")
loo_4
Computed from 4000 by 200 log-likelihood matrix.
Estimate SE
elpd_loo -462.2 22.9
p_loo 8.6 3.5
looic 924.4 45.9
------
MCSE of elpd_loo is 0.1.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.5, 1.1]).
All Pareto k estimates are good (k < 0.7).
See help('pareto-k-diagnostic') for details.loo() devuelve un objeto con varias métricas asociadas al ELPD. Para entender mejor cada una de ellas, se puede echar un vistazo al glosario de loo. elpd_loo es la estimación de ELPD mediante el método PSIS-LOO CV, para la cual también se tiene una medida de la variabilidad con un error estándar.
{loo} también provee la función loo_compare() que toma objetos devueltos por loo() y los ordena de mejor a peor según este criterio. En este caso se obtiene una estimación de la diferencia de ELPDs y un error estándar de la misma.
loo_compare(loo_1, loo_2, loo_3, loo_4) elpd_diff se_diff
model3 0.0 0.0
model4 -1.1 0.9
model1 -107.4 19.1
model2 -164.7 22.0 Según este criterio, el mejor modelo es el modelo 3. La diferencia de ELPD entre el modelo 3 y el modelo 1 es -107.4 y el error estándar de la misma es 19.2. Si se construye un intervalo aproximado del 95% restando y sumando 2 desvíos estándar de la estimación puntual, el mismo no cubre el 0 y se puede concluir que la diferencia de ELPDs entre el modelo 3 y el 1 es significativa.
Por otro lado, la diferencia de ELPD entre el modelo 3 y el modelo 4 es -1.1 con un error estándar de 0.9. Si se construye un intervalo aproximado del 95% de la misma forma que antes, el resultado cubre el 0 y se puede concluir que al diferencia de ELPDs entre el modelo 3 y el modelo 4 no es significativa. Como el modelo 3 es mas parsimonioso, se lo elige por sobre el modelo 4.