10 - Aproximación de grilla en 2 dimensiones

El siguiente programa muestra como se puede resolver en R el ejercicio Aproximación de grilla en 2 dimensiones de la Práctica 3.

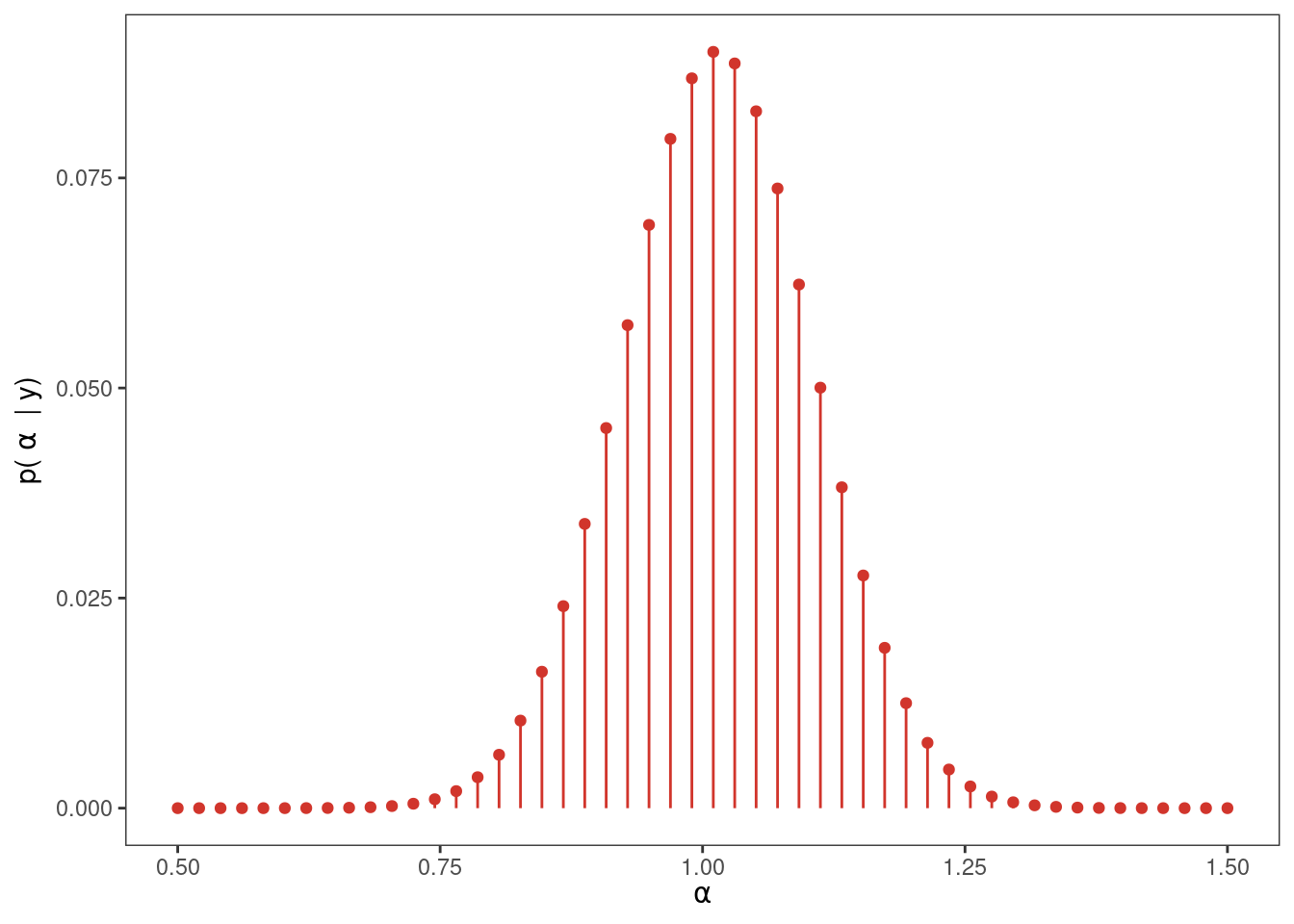
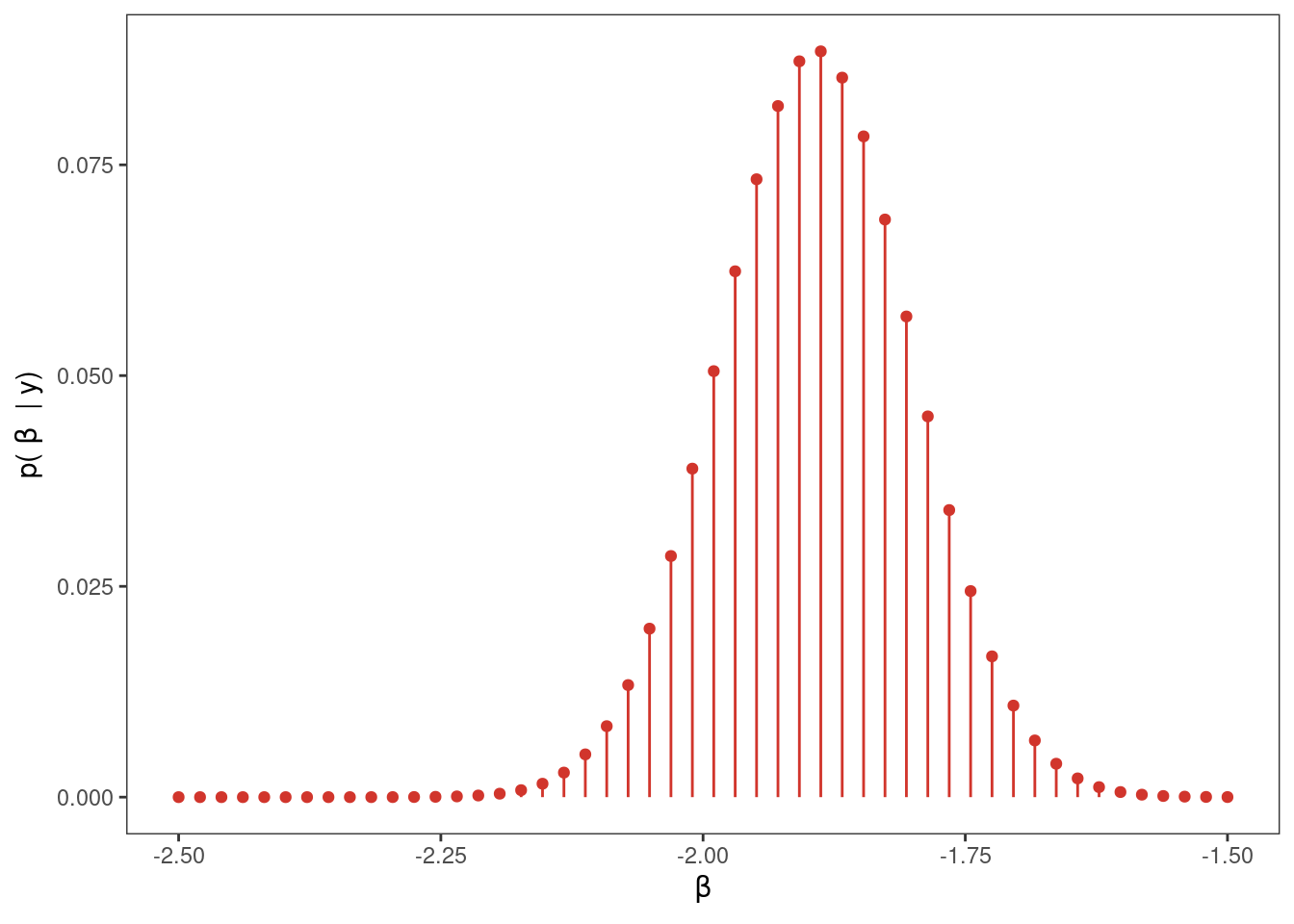
library(dplyr)
library(ggplot2)

set.seed(121195)

# Generación de datos
alpha <- 1
beta <- -2
sigma <- 0.8
n <- 80
x <- rnorm(n)
y <- rnorm(n, alpha + beta * x, sigma)
df <- data.frame(x = x, y = y)

# Crear grilla para alfa y beta
grid_a <- seq(0.5, 1.5, length.out = 50)
grid_b <- seq(-2.5, -1.5, length.out = 50)

# Crear todas las combinaciones entre los valores de las dos grillas
grid_df <- expand.grid(grid_a, grid_b)

# Utilizar nombres indicativos
names(grid_df) <- c("a", "b")

# Crear vectores que van a contener los valores de la
# función de verosimilitud y del posterior
likelihood <- numeric(nrow(grid_df))
posterior <- numeric(nrow(grid_df))

# Calcular la función de verosimilitud en cada punto
for (i in seq_along(likelihood)) {
    likelihood[i] <- prod(dnorm(y, grid_df$a[i] + grid_df$b[i] * x, sigma))
}
# Calcular el posterior en cada punto
posterior <- (
    likelihood
    * dnorm(grid_df$a, mean = 0, sd = 1.5) # alpha ~ Normal(0, 1.5)
    * dnorm(grid_df$b, mean = 0, sd = 2)   # beta ~ Normal(0, 2)
)

# Escalar el posterior para que sea propio
posterior <- posterior / sum(posterior)

# Incorporar likelihood y posterior al data frame
grid_df$likelihood <- likelihood
grid_df$posterior <- posterior

# Graficar con ggplot
ggplot(grid_df, aes(x = a, y = b)) +
    geom_raster(aes(fill = posterior)) +
    stat_contour(aes(z = posterior), col = "white", bins = 5) +
    geom_point(x = alpha, y = beta, color = "black", fill = "red", size = 3, pch = 21) +
    labs(x = expression(alpha), y = expression(beta)) +
    viridis::scale_fill_viridis() +
    guides(fill = guide_colourbar(barheight = unit(4.2, "in"))) +
    scale_x_continuous(expand = c(0, 0)) +
    scale_y_continuous(expand = c(0, 0))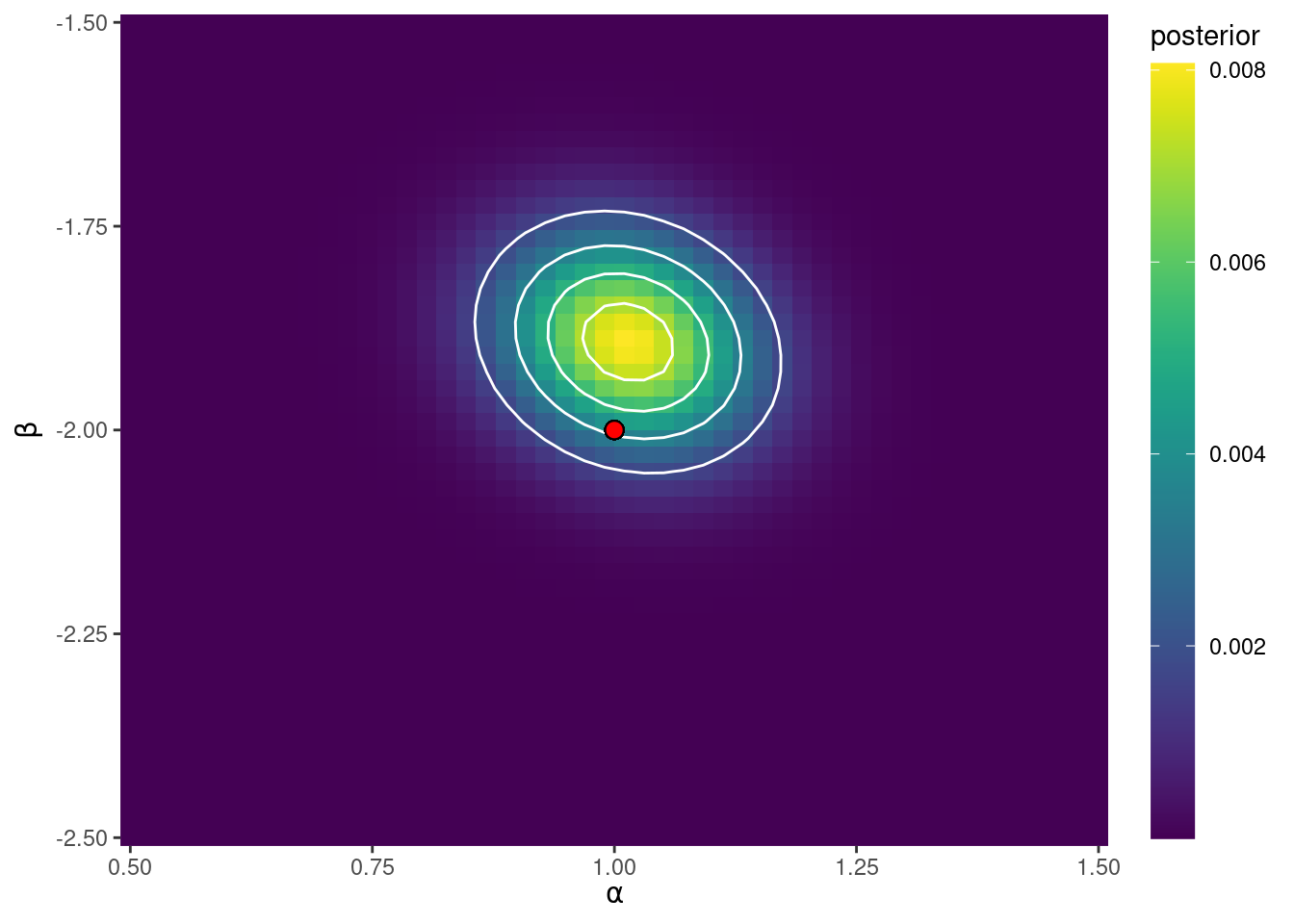

Distribución a posteriori evaluada en una grilla de 50×50 puntos.
El punto indica los valores de \(\alpha\) y \(\beta\) utilizados para generar los datos.

posterior_a_df <- grid_df |>
    group_by(a) |>
    summarise(p = sum(posterior))

ggplot(posterior_a_df) +
    geom_segment(aes(x = a, xend = a, y = 0, yend = p), color = "#d1352c") +
    geom_point(aes(x = a, y = p), color = "#d1352c") +
    labs(x = expression(alpha), y = expression("p(" ~ alpha ~ " | y)")) +
    theme_bw() +
    theme(
        panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
    )

Distribución marginal de \(\alpha\).

posterior_b_df <- grid_df |>
    group_by(b) |>
    summarise(p = sum(posterior))

ggplot(posterior_b_df) +
    geom_segment(aes(x = b, xend = b, y = 0, yend = p), color = "#d1352c") +
    geom_point(aes(x = b, y = p), color = "#d1352c") +
    labs(x = expression(beta), y = expression("p(" ~ beta ~ " | y)")) +
    theme_bw() +
    theme(
        panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
    )

Distribución marginal de \(\beta\).

\(P(\alpha > 0.95)\)

sum(posterior_a_df$p[posterior_a_df$a > 0.95])

[1] 0.7292537

\(P(\beta < -2)\)

sum(posterior_b_df$p[posterior_b_df$b < -2])

[1] 0.1204088