Este programa obtiene la distribución a posteriori para los diferentes casos del ejercicio ¿Quién domina el posterior ? de la Práctica 2.
Creamos dos funciones para simplificar los bloques de código en cada caso. La primera, generar_datos(), recibe una grilla para \(\pi\) , los valores de \(p(\pi)\) , \(p(y \mid \pi)\) y \(p(\pi, \mid y)\) en cada valor de la grilla, y devuelve un data.frame que permite graficar las 3 curvas con {ggplot2}. La segunda, generar_grafico(), simplemente toma el data.frame generado por generar_datos() y produce la visualización.
library (ggplot2)<- 200 <- seq (0 , 1 , length.out = grid_n)<- function (pi_grid, pi_prior, pi_likelihood, pi_posterior) {<- length (pi_grid)<- data.frame (x = rep (pi_grid, times = 3 ),y = c (pi_prior, pi_likelihood, pi_posterior),1 grupo = factor (rep (c ("prior" , "likelihood" , "posterior" ), each = grid_n),levels = c ("prior" , "likelihood" , "posterior" ),ordered = TRUE return (datos)<- function (datos) {<- c ("#f08533" , "#3b78b0" , "#d1352c" )<- ggplot (datos) + geom_line (aes (x = x, y = y, color = grupo), linewidth = 1 ) + scale_color_manual (values = colores) + labs (x = expression (pi), y = NULL ) + facet_wrap (~ grupo, scales = "free_y" ) + theme_bw () + theme (panel.grid.major = element_blank (),panel.grid.minor = element_blank (),axis.ticks.y = element_blank (),axis.text.y = element_blank (),legend.position = "none" return (plt)
1
Se usa un factor() ordenado para indicarle a {ggplot2} que primero se ubica el prior , luego el likelihood , y finalmente el posterior .
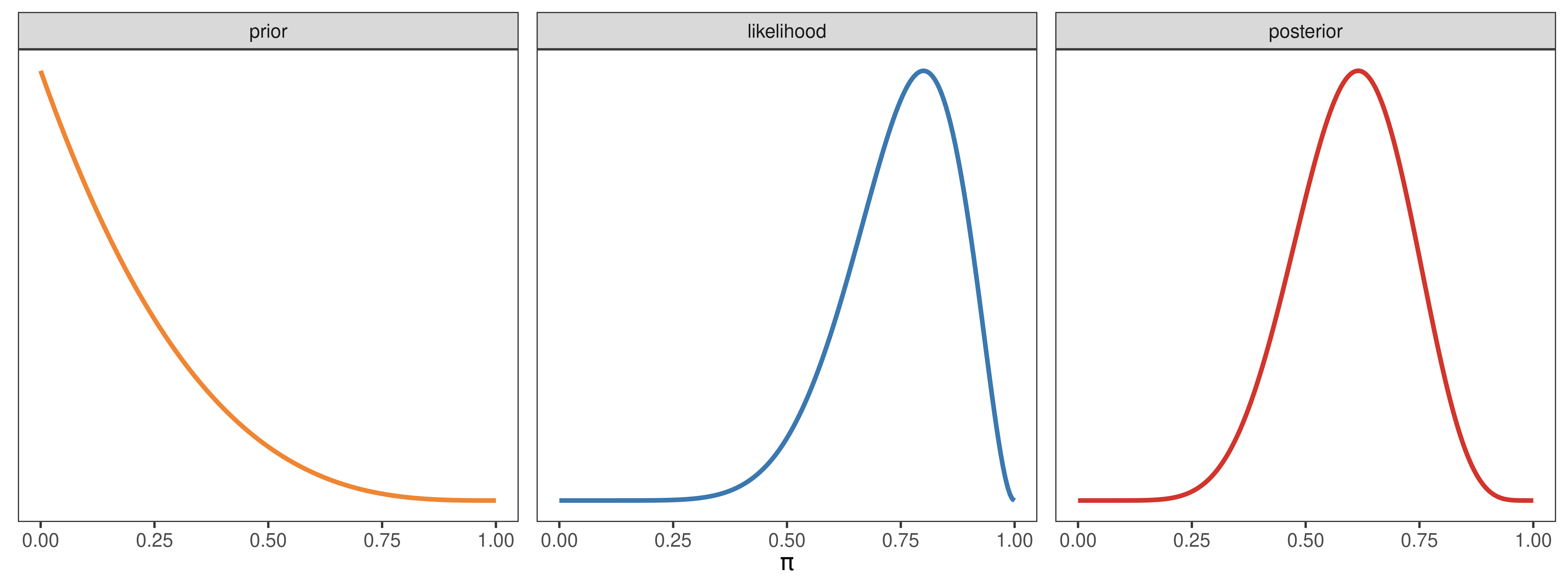
Caso i
<- 1 <- 4 <- 8 <- 10 <- dbeta (pi_grid, a_prior, b_prior)<- dbinom (y, N, pi_grid)<- dbeta (pi_grid, a_prior + y, b_prior + N - y)<- generar_datos (pi_grid, pi_prior, pi_likelihood, pi_posterior)generar_grafico (datos)
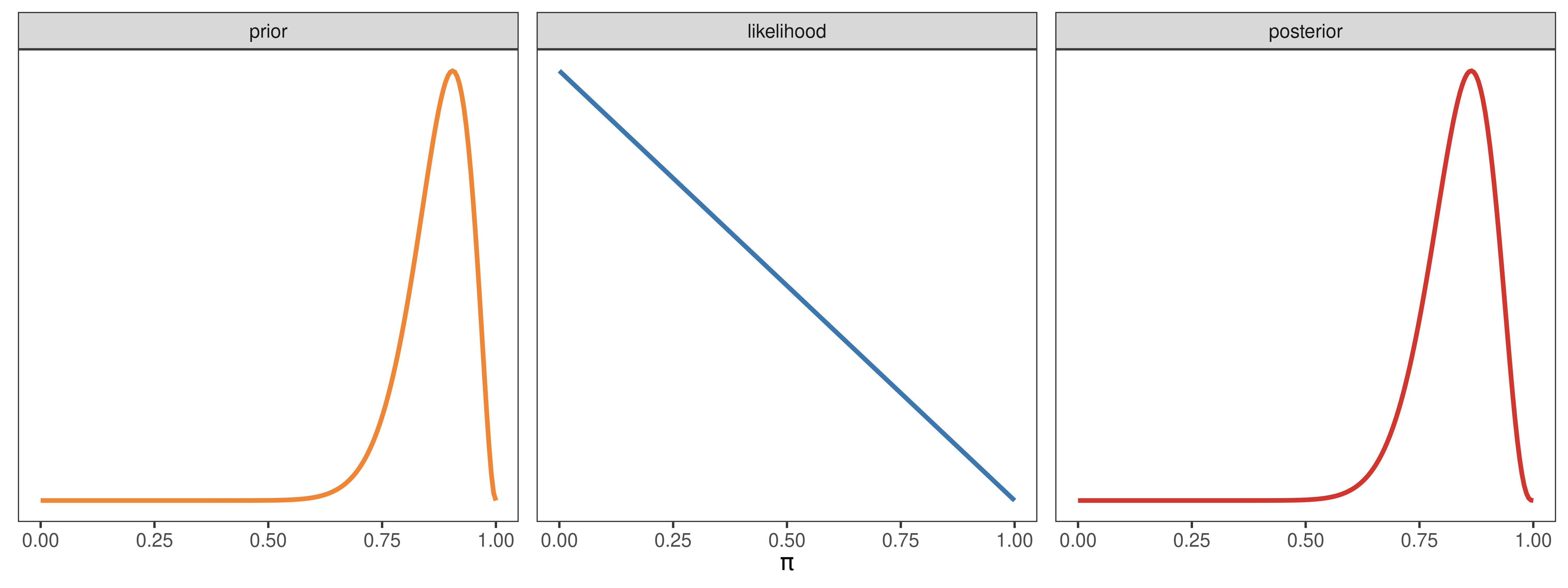
Caso ii
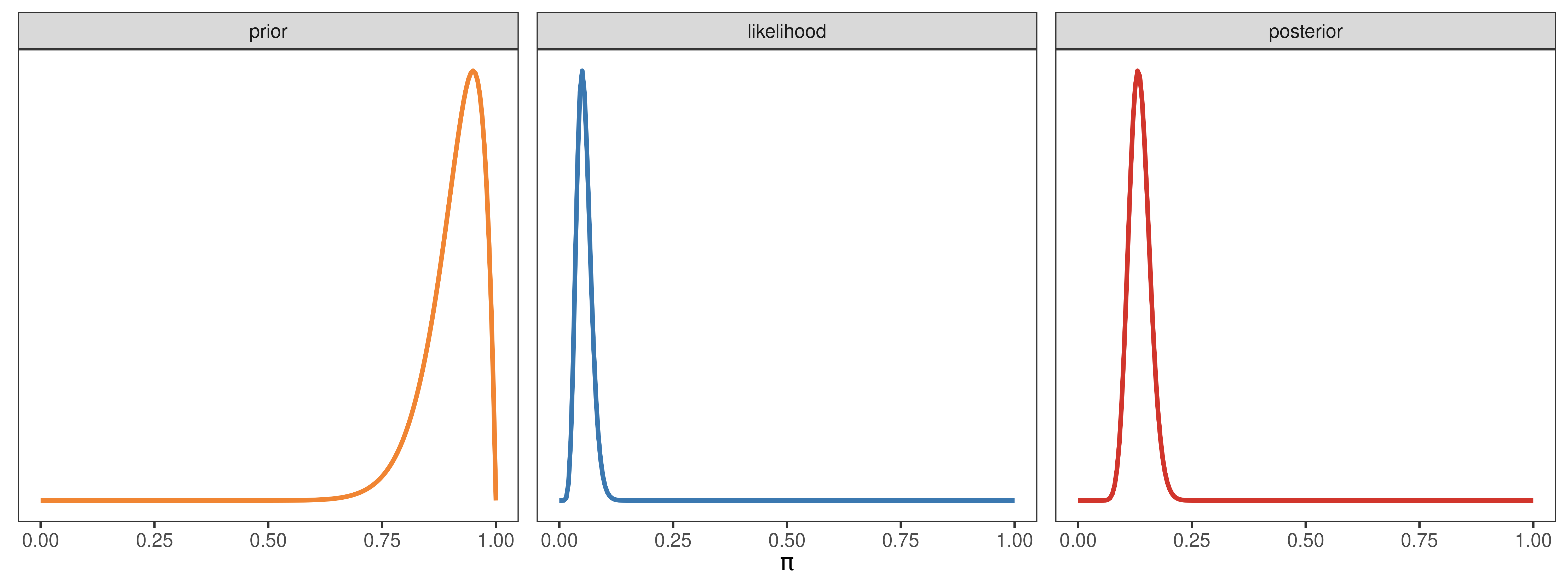
<- 20 <- 3 <- 0 <- 1 <- dbeta (pi_grid, a_prior, b_prior)<- dbinom (y, N, pi_grid)<- dbeta (pi_grid, a_prior + y, b_prior + N - y)<- generar_datos (pi_grid, pi_prior, pi_likelihood, pi_posterior)generar_grafico (datos)
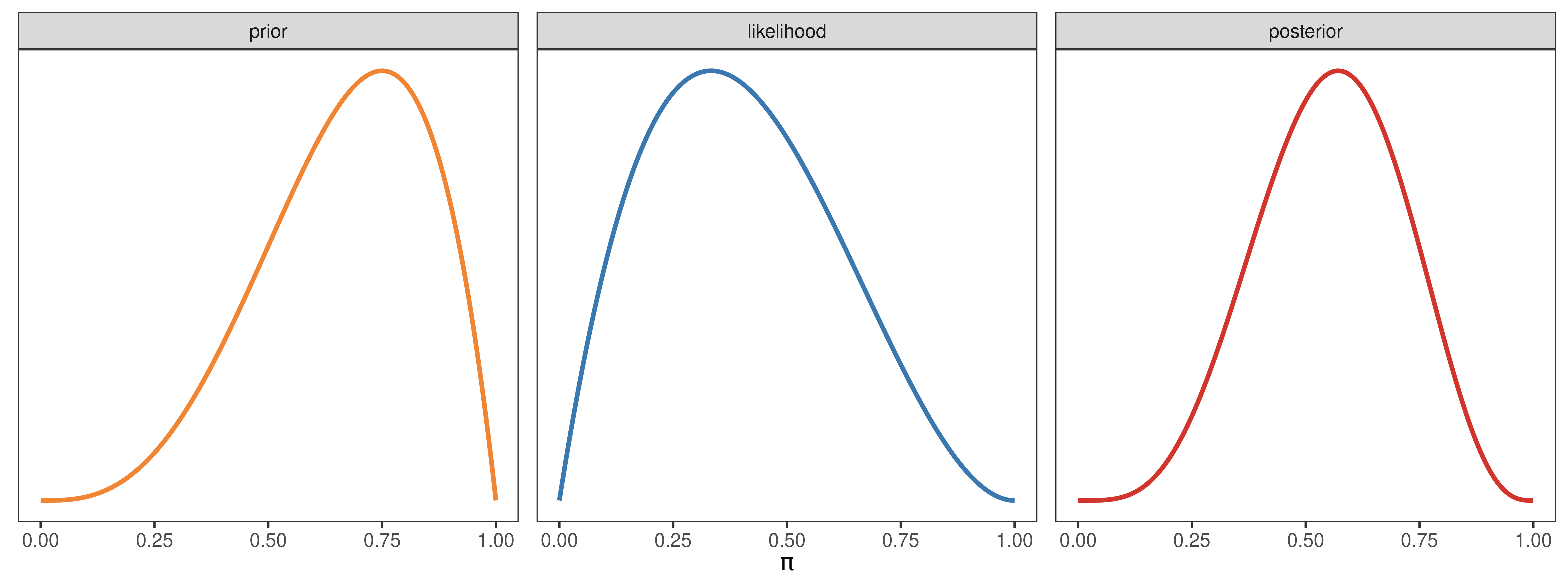
Caso iii
<- 4 <- 2 <- 1 <- 3 <- dbeta (pi_grid, a_prior, b_prior)<- dbinom (y, N, pi_grid)<- dbeta (pi_grid, a_prior + y, b_prior + N - y)<- generar_datos (pi_grid, pi_prior, pi_likelihood, pi_posterior)generar_grafico (datos)
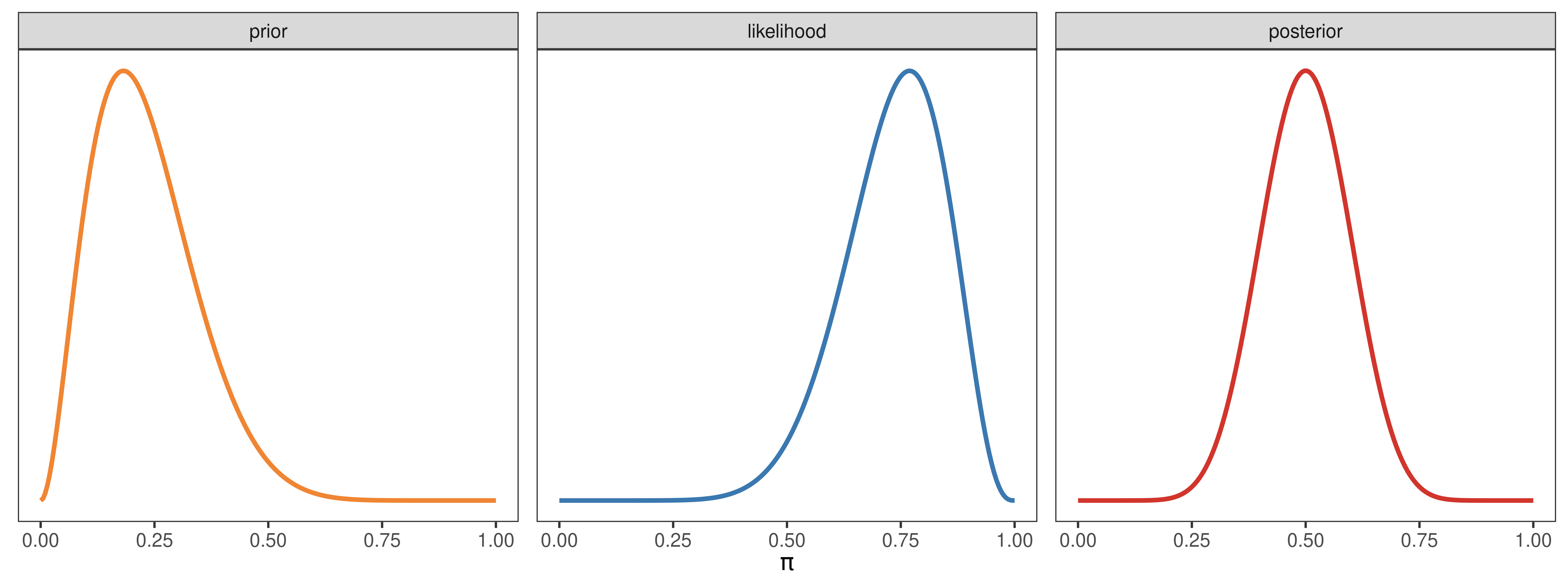
Caso iv
<- 3 <- 10 <- 10 <- 13 <- dbeta (pi_grid, a_prior, b_prior)<- dbinom (y, N, pi_grid)<- dbeta (pi_grid, a_prior + y, b_prior + N - y)<- generar_datos (pi_grid, pi_prior, pi_likelihood, pi_posterior)generar_grafico (datos)
Caso v
<- 20 <- 2 <- 10 <- 200 <- dbeta (pi_grid, a_prior, b_prior)<- dbinom (y, N, pi_grid)<- dbeta (pi_grid, a_prior + y, b_prior + N - y)<- generar_datos (pi_grid, pi_prior, pi_likelihood, pi_posterior)generar_grafico (datos)