05 - Función de verosimilitud Poisson

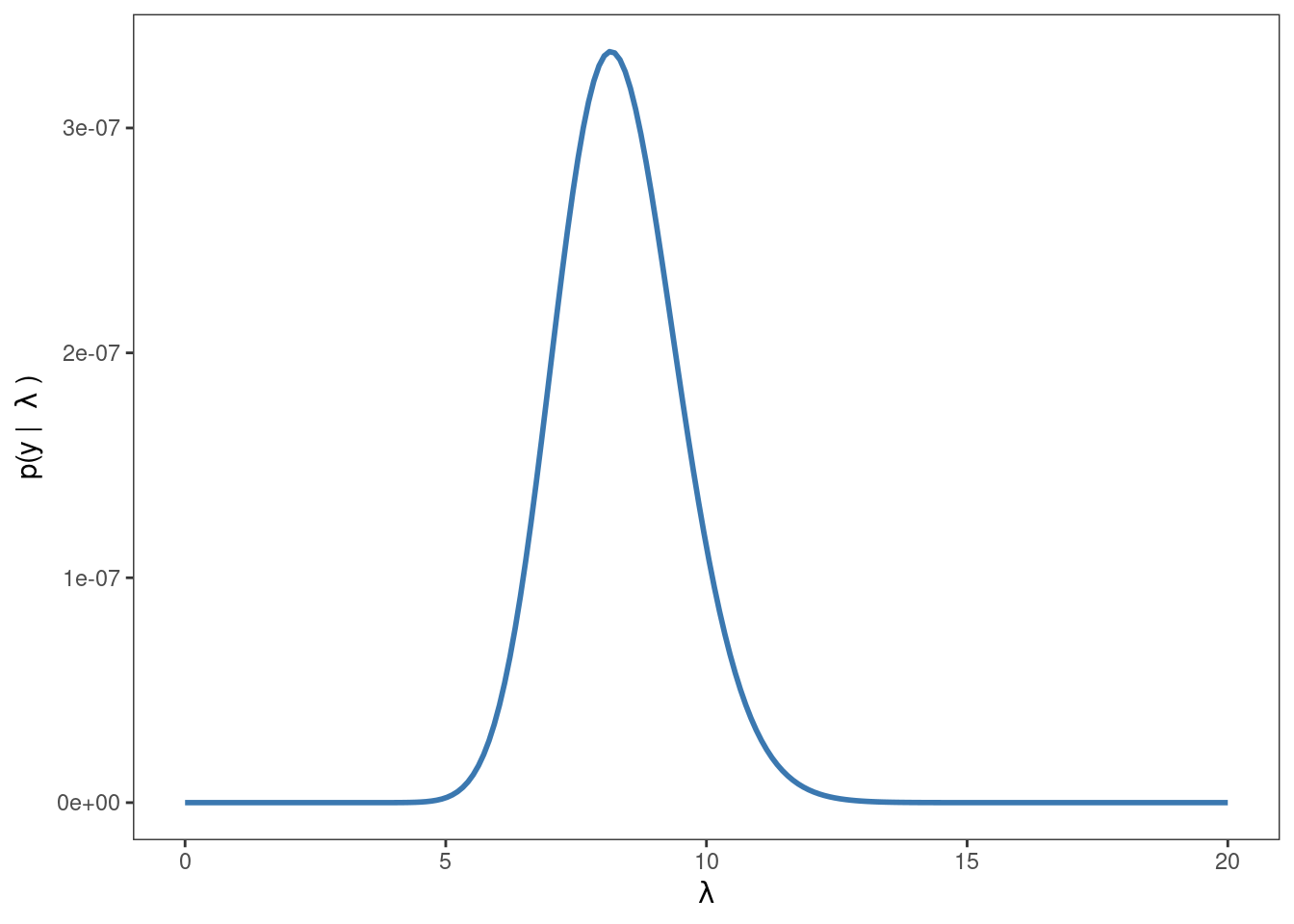
Este programa grafica la función de verosimilitud cuando se obtiene una muestra de \(n\) realizaciones independientes de una distribución Poisson. Se utiliza en el ejercicio El modelo Gamma-Poisson de la Práctica 2.

\[ \begin{array}{lcc} X \sim \text{Poisson}(\lambda), & \lambda > 0, & X \in \{0, 1, 2, \cdots \} \end{array} \]

\[ p(x \mid \lambda) = \frac{e^{-\lambda} \lambda^x}{x!} \]

\[ \ell(\theta \mid x_1, x_2, \cdots, x_n) = p(\mathbf{x} \mid \theta) = \prod_{i=1}^{n} p(x_i \mid \lambda) = \prod_{i=1}^{n} \frac{e^{-\lambda} \lambda^{x_i}}{x_i!} = \frac{e^{- n \lambda} \lambda^{\sum_i x_i}}{\prod_i x_i!} \]

library(ggplot2)

# Cantidad de mensajes observados
mensajes <- c(7, 3, 8, 9, 10, 12)

Opción 1: Escribir la función de verosimilitud analíticamente

n <- length(mensajes)
total <- sum(mensajes)
producto_factoriales <- prod(factorial(mensajes))

# Grilla de valores para 'lambda'
# Teoréticamente, el soporte del parámetro es (0, infty). Lo acotamos en 20.
lambda <- seq(0, 20, length.out = 200)

# Cálculo de la verosimilitud
verosimilitud <- exp(-n * lambda) * lambda ^ total / producto_factoriales

# Visualización de la verosimilitud para los valores de lambda en la grilla
data.frame(x = lambda, y = verosimilitud) |>
    ggplot() +
    geom_line(aes(x = x, y = y), linewidth = 1, color = "#3b78b0") +
    labs(x = expression(lambda), y = expression("p(y | " ~ lambda ~ ")")) +
    theme_bw() +
    theme(
        panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
    )

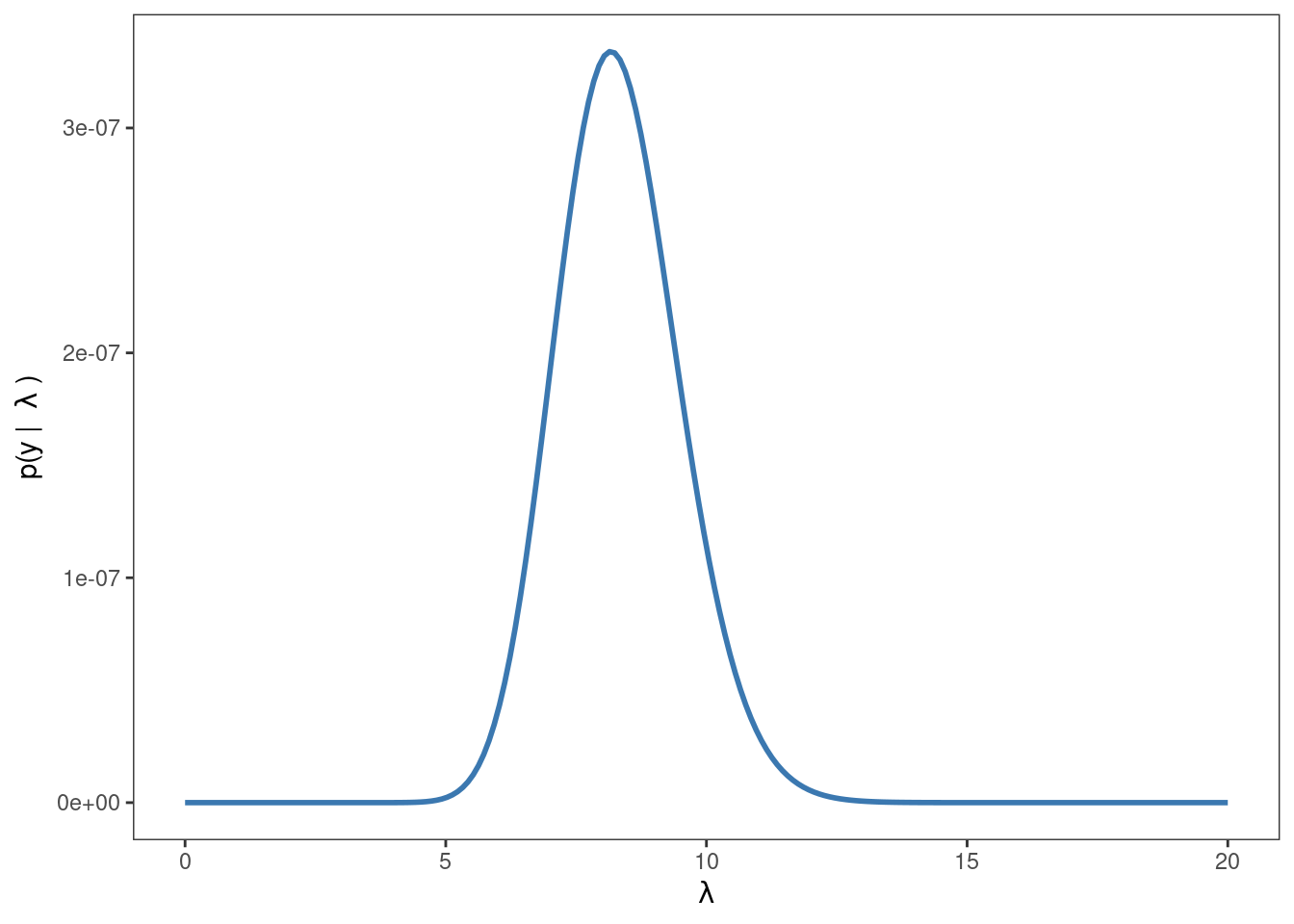
Opción 2: Utilizar dpois

mensajes_matriz <- matrix(rep(mensajes, 200), nrow = 200, byrow = TRUE)
1pmf <- dpois(mensajes_matriz, lambda)
2verosimilitud <- apply(pmf, 1, prod)

data.frame(x = lambda, y = verosimilitud) |>
    ggplot() +
    geom_line(aes(x = x, y = y), linewidth = 1, color = "#3b78b0") +
    labs(x = expression(lambda), y = expression("p(y | " ~ lambda ~ ")")) +
    theme_bw() +
    theme(
        panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
    )

1: Evaluar la función de masa de probabilidad de la distribución Poisson en cada uno de los valores observados utilizando una grilla de valores de \(\lambda\).
2: Para cada valor de \(\lambda\), multiplicar todas las evaluaciones realizadas.