01 - Liberen al Tucán Sam

En este recurso se muestra como usar R para resolver el ejercicio de los Froot Loops hecho durante la primera clase.

library(ggplot2)
library(patchwork)

colores <- c("#f08533", "#3b78b0", "#d1352c")

En base al prior elicitado grupalmente en clase:

# Determinar grilla de puntos
pi_grid <- seq(0, 1, length.out = 11)
print(pi_grid)
 [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
# Especificar prior
# Tenemos $1000 y los dividimos en los diferentes valores de "pi"
prior_ <- c(0, 50, 150, 600, 150, 50, 0, 0, 0, 0, 0)
prior <- prior_ / sum(prior_)

# Recolectar datos
cantidad_de_cereales <- 29 # n
cantidad_de_cereales_amarillos <- 7 # y

# Calcular verosimilitud para cada valor de "pi" en la grilla
likelihood <- dbinom(
  cantidad_de_cereales_amarillos,
  cantidad_de_cereales,
  pi_grid
)

# Obtener posterior
posterior_ <- prior * likelihood
posterior <- posterior_ / sum(posterior_) # normalización

# Graficar prior
plt_prior <- data.frame(x = pi_grid, y = prior) |>
  ggplot() +
  geom_segment(aes(x = x, xend = x, y = 0, yend = y), color = colores[1], linewidth = 0.8) +
  geom_point(aes(x = x, y = y), , color = colores[1], size = 2.4) +
  scale_x_continuous(breaks = pi_grid) +
  labs(
    x = expression(pi),
    y = expression(p ~ "(" ~ pi ~ ")"),
    title = "Distribución a priori"
  ) +
  theme_bw() +
  theme(panel.grid.minor = element_blank())

# Graficar verosimilitud
plt_likelihood <- data.frame(x = pi_grid, y = likelihood) |>
  ggplot() +
  geom_segment(aes(x = x, xend = x, y = 0, yend = y), color = colores[2], linewidth = 0.8) +
  geom_point(aes(x = x, y = y), , color = colores[2], size = 2.4) +
  scale_x_continuous(breaks = pi_grid) +
  labs(
    x = expression(pi),
    y = expression(p ~ "(y | " ~ pi ~ ")"),
    title = "Función de verosimilitud"
  ) +
  theme_bw() +
  theme(panel.grid.minor = element_blank())

# Graficar posterior
plt_posterior <- data.frame(x = pi_grid, y = posterior) |>
  ggplot() +
  geom_segment(aes(x = x, xend = x, y = 0, yend = y), color = colores[3], linewidth = 0.8) +
  geom_point(aes(x = x, y = y), , color = colores[3], size = 2.4) +
  scale_x_continuous(breaks = pi_grid) +
  labs(
    x = expression(pi),
    y = expression(p ~ "(" ~ pi ~ " | y)"),
    title = "Distribución a posteriori"
  ) +
  theme_bw() +
  theme(panel.grid.minor = element_blank())

# Concatenar graficos
plt_prior | plt_likelihood | plt_posterior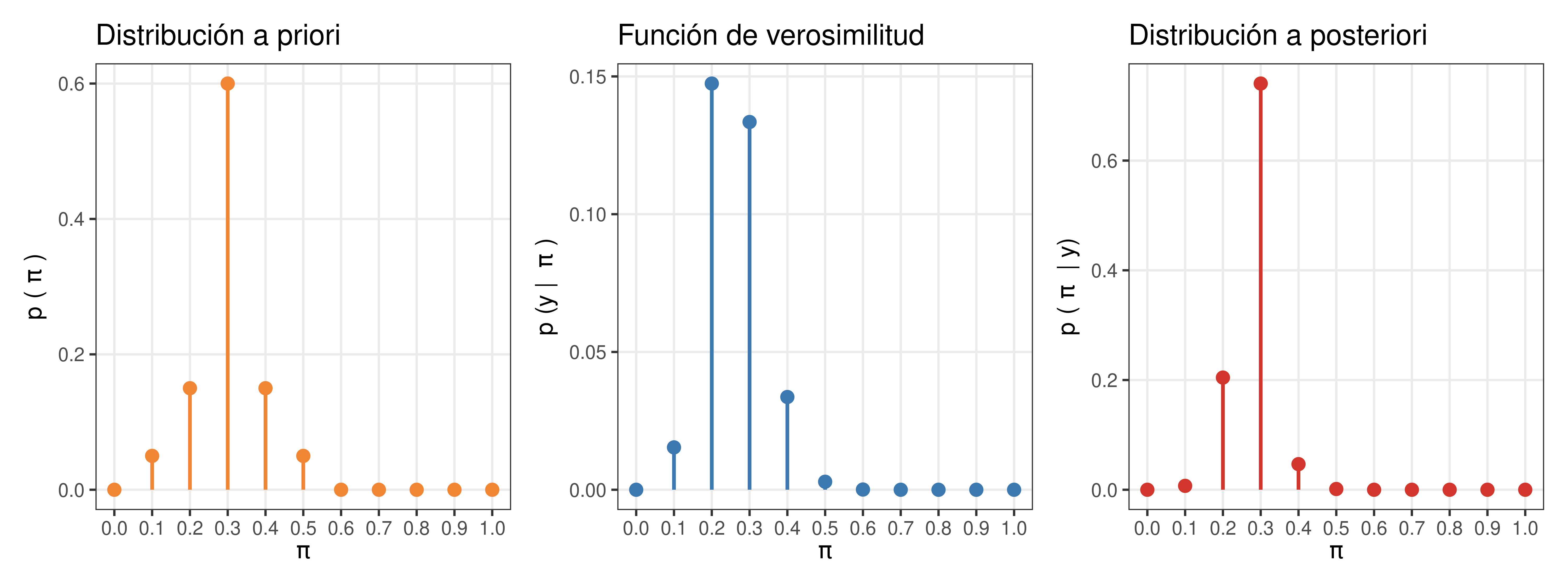

En base a un prior beta:

# Determinar grilla de puntos
pi_grid <- seq(0, 1, length.out = 200)

# Obtener prior
prior_ <- dbeta(pi_grid, 3, 7)
prior <- prior_ / sum(prior_)

# Calcular verosimilitud para cada valor de "pi"
likelihood <- dbinom(
  cantidad_de_cereales_amarillos,
  cantidad_de_cereales,
  pi_grid
)

# Obtener posterior
posterior_ <- prior * likelihood
posterior <- posterior_ / sum(posterior_)

# Graficar prior
plt_prior <- data.frame(x = pi_grid, y = prior) |>
  ggplot() +
  geom_line(aes(x = x, y = y), color = colores[1], linewidth = 1) +
  labs(
    x = expression(pi),
    y = expression(p ~ "(" ~ pi ~ ")"),
    title = "Distribución a priori"
  ) +
  theme_bw() +
  theme(panel.grid.minor = element_blank())

# Graficar verosimilitud
plt_likelihood <- data.frame(x = pi_grid, y = likelihood) |>
  ggplot() +
  geom_line(aes(x = x, y = y), color = colores[2], linewidth = 1) +
  labs(
    x = expression(pi),
    y = expression(p ~ "(y | " ~ pi ~ ")"),
    title = "Función de verosimilitud"
  ) +
  theme_bw() +
  theme(panel.grid.minor = element_blank())

# Graficar posterior
plt_posterior <- data.frame(x = pi_grid, y = posterior) |>
  ggplot() +
  geom_line(aes(x = x, y = y), color = colores[3], linewidth = 1) +
  labs(
    x = expression(pi),
    y = expression(p ~ "(" ~ pi ~ " | y)"), 
    title = "Distribución a posteriori"
  ) +
  theme_bw() +
  theme(panel.grid.minor = element_blank())

# Concatenar graficos
plt_prior | plt_likelihood | plt_posterior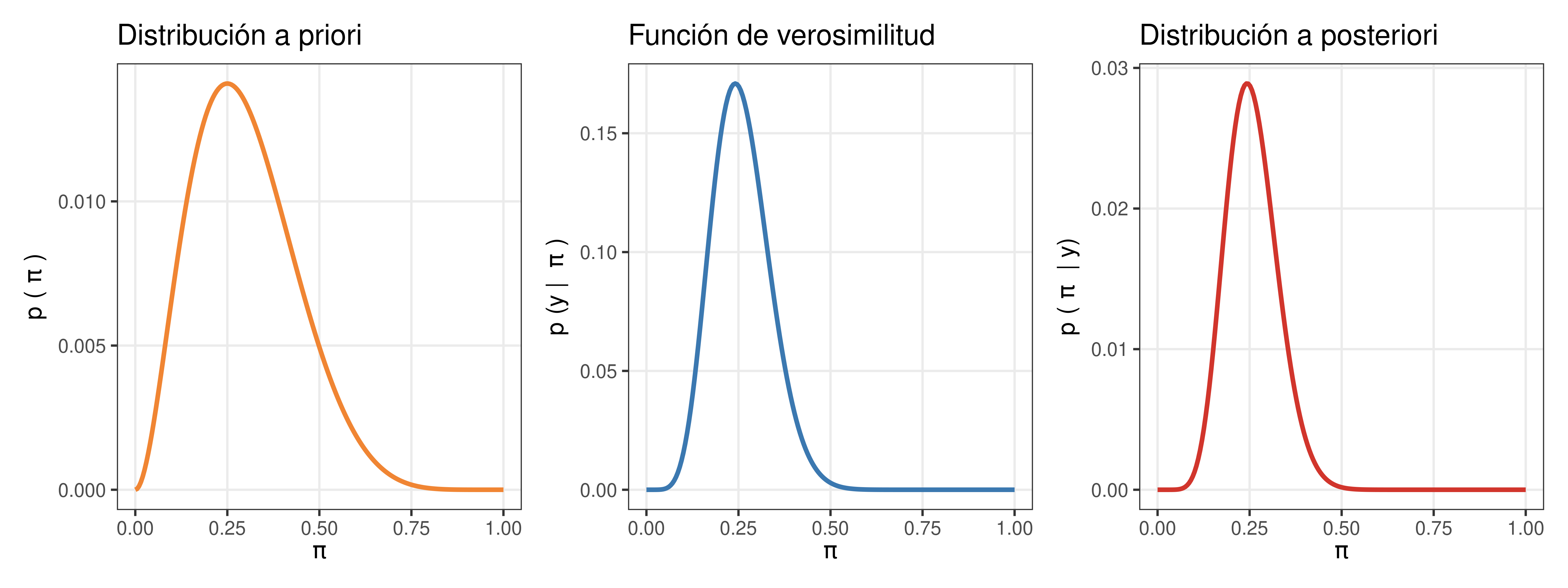

Preguntas