24  Arreglos

En este capítulo vamos a trabajar con arreglos, una clase de estructuras que agrupan múltiples datos en una mismo objeto y los organizan en una o más dimensiones. Vamos a empezar con los vectores, que son arreglos unidimensionales, y luego avanzaremos hacia las matrices, que extienden la idea a dos dimensiones. También veremos cómo se pueden añadir atributos a los objetos en R para guardar información adicional, como los nombres de las dimensiones. Nos enfocaremos en cómo acceder, modificar y operar sobre los elementos de estas estructuras con instrucciones claras y detalladas.

Hasta ahora todos los programas que hemos desarrollado hacen uso de objetos que guardan datos individuales, los cuales representan un número, una cadena de texto o un valor lógico. Sin embargo, la verdadera utilidad de la computación radica en poder trabajar con muchos datos a la vez, organizados de acuerdo a ciertas reglas que permitan su manipulación y acceso.

En el contexto de la programación, una estructura de datos es una forma organizada de almacenar y manipular datos dentro de un programa informático. Permite a los desarrolladores organizar y gestionar información de manera eficiente, optimizando el acceso y la manipulación de los datos para resolver problemas específicos.

Hay muchos tipos de estructuras de datos y cada lenguaje de programación propone los suyos propios. Sin embargo, las estructuras más sencillas se conocen como arreglos y de una u otra forma están presentes en todos los lenguajes, permitiendo generalizar su definición.

Un arreglo (también conocido como array) es una estructura de datos que permite almacenar una colección ordenada de elementos. En la mayoría de los lenguajes, los elementos de un arreglo son del mismo tipo, lo que permite realizar operaciones de forma eficiente y sistemática sobre todos ellos. Por ejemplo, un arreglo puede contener únicamente números, caracteres o valores lógicos, según cómo haya sido definido. De esta forma, decimos que los arreglos tienen dos características fundamentales:

  • Ordenamiento: los elementos individuales pueden ser enumerados en orden, es decir, debe ser posible identificar en qué posición del arreglo se encuentra cada valor (qué hay en primer lugar, qué hay en segundo lugar, etc.).
  • Homogeneidad: los elementos individuales almacenados en un arreglo son del mismo tipo (numérico, carácter, lógico).

Los arreglos son muy útiles para almacenar información en la memoria de la computadora, organizando valores que estén relacionados entre sí de alguna manera, por ejemplo, un conjunto de precios, los meses del año, el listado de calificaciones de estudiantes en distintos parciales, etc.

Para indicar qué posición ocupa cada elemento en el arreglo se emplean uno o más índices. Dependiendo de cuántos índices se deban utilizar para acceder a cada elemento dentro de los arreglos, estos se clasifican en unidimensionales (vectores), bidimensionales (matrices) o multidimensionales.

La homogeneidad de los arreglos no solo simplifica las operaciones sobre los elementos, sino que también permite al lenguaje de programación realizar una gestión más eficiente de la memoria. En los arreglos clásicos, los elementos se almacenan en posiciones contiguas de memoria, lo que posibilita un acceso rápido a cualquier valor. Esta propiedad se mantiene en muchos lenguajes, incluyendo R.

24.1 Vectores

Un vector es la estructura de datos más simple y fundamental en R. Se trata de un arreglo unidimensional que, como tal, sólo posee elementos del mismo tipo: todos numéricos, todos de texto, todos lógicos, etc. Por ejemplo, el siguiente es un vector de tipo numérico llamado x con 5 elementos:

Ejemplo de un vector numérico.

Ejemplo de un vector numérico.

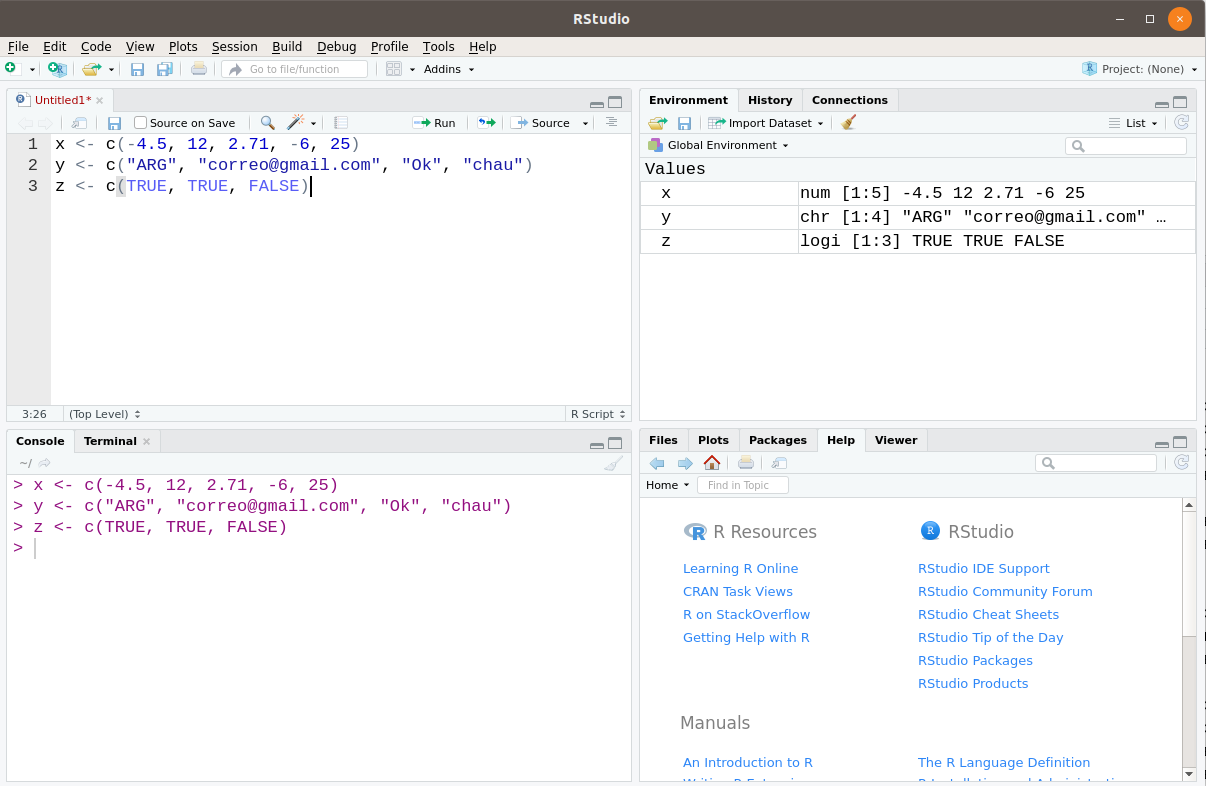
En R, los vectores se construyen con la función c() (de combine), que reúne una serie de valores en una única estructura. Para guardar un vector en nuestro ambiente global, necesitamos elegir un nombre y utilizar el operador de asignación <-:

x <- c(-4.5, 12, 2.71, -6, 25)

Cuando ejecutamos la línea anterior, se crea en el ambiente global el objeto x, como podemos notar en la pestaña Environment de RStudio. Es decir, los arreglos son objetos que constituyen entidades en sí mismas y que pueden ser manipulados al hacer referencia a sus nombres. Además, RStudio nos muestra en la pestaña mencionada qué tipo de vector es cada uno (en este caso dice num), cuántos elementos tiene (pone [1:5]) y una previsualización de sus primeros elementos. También podemos chequear el tipo de vector y la cantidad de elementos que tiene en la consola:

typeof(x)
[1] "double"
length(x)
[1] 5

Cada uno de los elementos ocupa una posición determinada en el vector. Por ejemplo, el elemento 3 del vector x es el numéro 2.71. Se puede acceder o hacer referencia (indexar) a cada elemento mediante el uso de un índice, expresado con un número entero entre corchetes al lado del nombre del vector. De esta forma, si escribimos x[3] hacemos referencia a la tercera posición del vector, que actualmente guarda al valor 2.71. Como podemos ver, sólo hace falta un índice para hacer referencia a cada elemento de un vector.

Ejemplo de un vector numérico: se necesita de un solo índice para señalar cada posición.

Ejemplo de un vector numérico: se necesita de un solo índice para señalar cada posición.
x[1]
[1] -4.5
x[3]
[1] 2.71
x[2] + x[5]
[1] 37
x[4] * 2
[1] -12

En R, este tipo de estructura se denomina técnicamente vector atómico o atomic vector, concepto que ya presentamos en la Unidad 1. En aquella oportunidad, dijimos que este es el nombre que R le da al tipo de objeto más simple y básico; que hay seis tipos de vectores atómicos según los datos que guardan (doubles, characters, logicals, etc.); y que por el momento trabajaríamos con vectores atómicos que sólo contenían un valor almacenado. Ahora ha llegado el momento de sacarle más provecho a estas estructuras de datos, sabiendo que pueden guardar uno o más valores. Como ya sabemos, cuando definimos una variable que sólo guarda un valor, también estamos creando un vector atómico, con la particularidad de que su largo es igual a 1 y, por lo tanto, el uso del índice [1] se puede omitir:

# Defino una variable numérica: es un objeto simple, llamado "vector atómico"
precio <- 100
is.vector(precio)
[1] TRUE
# Es un vector de tipo double
typeof(precio)
[1] "double"
# Es un vector de largo 1, tien un solo dato
length(precio)
[1] 1
# Por comodidad, no usamos un índice para operar con el único valor almacenado
precio * 1.10
[1] 110
# Pero podríamos hacerlo y sería lo mismo
precio[1] * 1.10
[1] 110

Desde ahora usaremos vectores atómicos para guardar cualquier cantidad de elementos. Veamos ejemplos de vectores atómicos de tipo carácter y lógico, con distintos largos:

Ejemplo de un vector carácter y un vector lógico.

Ejemplo de un vector carácter y un vector lógico.

Los definimos en R:

y <- c("ARG", "correo@gmail.com", "Ok", "chau")
z <- c(TRUE, TRUE, FALSE)

Creación de vectores en R.

Creación de vectores en R.

Inspeccionamos su tipo y contenido, y vemos que podemos hacer algunas operaciones con ellos:

typeof(y)
[1] "character"
length(y)
[1] 4
nchar(y[2])
[1] 16
typeof(z)
[1] "logical"
length(z)
[1] 3
z[1] && z[2]
[1] TRUE

Podemos emplear estructuras iterativas para recorrer todas las posiciones de un vector y realizar operaciones con ellas, por ejemplo:

suma <- 0
for (i in 1:5) {
  cat("La posición", i, "de x está ocupada por el valor", x[i], "\n")
  cat(x[i], "al cuadrado es igual a", x[i]^2, "\n")
  suma <- suma + x[i]
}
cat("La suma de los elementos del vector x es igual a", suma)
La posición 1 de x está ocupada por el valor -4.5 
-4.5 al cuadrado es igual a 20.25 
La posición 2 de x está ocupada por el valor 12 
12 al cuadrado es igual a 144 
La posición 3 de x está ocupada por el valor 2.71 
2.71 al cuadrado es igual a 7.3441 
La posición 4 de x está ocupada por el valor -6 
-6 al cuadrado es igual a 36 
La posición 5 de x está ocupada por el valor 25 
25 al cuadrado es igual a 625 
La suma de los elementos del vector x es igual a 29.21

En el ejemplo anterior, se estableció que i itere entre 1 y 5 (i in 1:5) para recorrer desde el primer al último elemento de x. Es mucho mejor establecer el recorrido de la variable de iteración en función del largo de x, para que el código sirva sea cual sea la cantidad de elementos en este vector:

suma <- 0
for (i in 1:length(x)) {
  cat("La posición", i, "de x está ocupada por el valor", x[i], "\n")
  cat(x[i], "al cuadrado es igual a", x[i]^2, "\n")
  suma <- suma + x[i]
}
cat("La suma de los elementos del vector x es igual a", suma)

En relación al comentario anterior, hay otra recomendación para tener en cuenta: las buenas prácticas recomiendan reemplazar 1:length(x) por seq_along(x). Ambas formas producen el mismo resultado, un vector de valores entre 1 y la cantidad de elementos de x, pero la segunda es más segura, porque puede prevenir de cometer errores, especialmente cuando existe la posibilidad de que x sea un vector vacío.

Supongamos que x <- c(), es decir, un vector vacío. Si calculamos length(x), da 0. Entonces, 1:length(x) se convierte en 1:0, que es una secuencia numérica descendente: 1, 0 y el bucle for (i in 1:length(x)) se ejecuta con valores 1 y 0, que no son índices válidos para x. Esto puede llevar a errores sutiles o comportamientos inesperados, como:

# Vector vacío
x <- c()
# Largo del vector
length(x)
[1] 0
# Valores para i
1:length(x)
[1] 1 0
# Comportamiento no deseado: se ejecuta e imprime NULL
for (i in 1:length(x)) {
  print(x[i])
}
NULL
NULL

En cambio, seq_along(x) da una secuencia vacía si x está vacío, y el bucle no se ejecuta, que es el comportamiento esperado:

# Vector vacío
x <- c()
# Largo del vector
length(x)
[1] 0
# Valores para i: ninguno
seq_along(x)
integer(0)
# Comportamiento deseado: no se ejecuta
for (i in seq_along(x)) {
  print(x[i])
}

seq_along(x) comunica de manera clara que vamos a recorrer los índices válidos de x. Es una función pensada específicamente para este uso. Asegura que el código se comporte correctamente tanto si x tiene muchos elementos, como si tiene uno solo o está vacío.

Antes comentamos que en R los vectores se crean con expresiones como x <- c(-4.5, 12, 2.71, -6, 25), donde sus elementos están listados de forma literal. También podemos crear vectores de un largo determinado dejando que cada posición quede ocupada por algún valor asignado por defecto. Por ejemplo, el siguiente código crea un vector de tipo numérico con 10 posiciones, uno carácter con 7 y otro lógico con 2. En cada caso, R rellena todas las posiciones con el mismo valor: ceros, caracteres vacíos "" y valores FALSE, respectivamente:

a <- numeric(10)
b <- character(7)
d <- logical(2)

a
 [1] 0 0 0 0 0 0 0 0 0 0
b
[1] "" "" "" "" "" "" ""
d
[1] FALSE FALSE

Sin ejecutar el código, determinar cuál será el contenido del vector a al finalizar:

a <- numeric(10)
for (i in 1:length(a)) {
    if (i %% 3 == 0) {
        a[i] <- i * 100
    }
}
a

Invertir de lugar los elementos de un vector

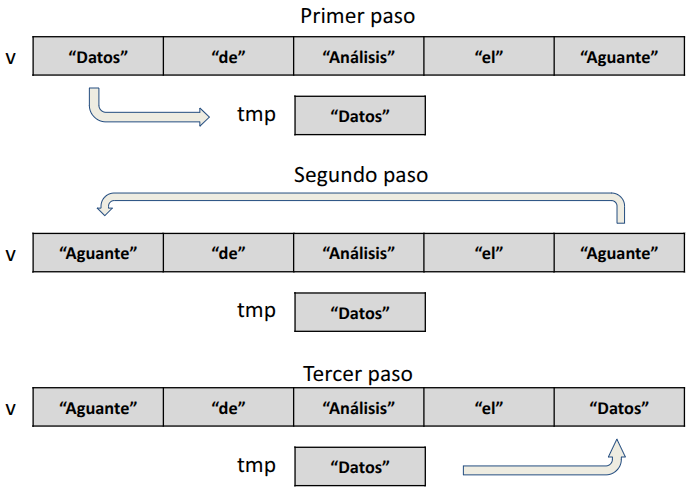
Nos planteamos el problema de dar vuelta los elementos pertenecientes a un vector, de manera que el primer elemento pase a ser el último, el segundo pase al penúltimo lugar, etc. Por ejemplo, dado el vector de tipo carácter v:

Vector v.

Vector v.

queremos modificarlo para obtener:

Resultado buscado.

Resultado buscado.

Si bien podemos pensar en distintas formas para resolver este problema, probablemente la más sencilla requiere que intercambiemos de a dos los valores en ciertas posiciones del vector, empezando por intercambiar el primero con el último. Para esto podemos emplear una variable auxiliar que guarde el valor de alguna de las celdas temporalmente (por eso lo vamos a llamar tmp):

Pasos para intercambiar los valores entre la primera y última posición.

Pasos para intercambiar los valores entre la primera y última posición.

Ahora sólo resta realizar el mismo procedimiento para los valores de las posiciones 2 y 4. Como el número de elementos en el vector es impar, el valor en la posición central queda en su lugar. Podemos definir el siguiente programa para resolver este problema de manera general, para vectores de cualquier largo n:

v <- c("Datos", "de", "Análisis", "el", "Aguante")
n <- length(v)
for (i in 1:(n %/% 2)) {
    tmp <- v[i]
    v[i] <- v[n - i + 1]
    v[n - i + 1] <- tmp
}
v
[1] "Aguante"  "el"       "Análisis" "de"       "Datos"

En R, la indexación de los elementos de un vector comienza en 1, lo que significa que el primer elemento se accede con x[1]. Este enfoque se conoce como indexación basada en uno o 1-indexed. Sin embargo, muchos otros lenguajes de programación populares (como C, C++, Java, Python y JavaScript) utilizan indexación basada en cero (0-indexed), donde el primer elemento se accede con x[0]. Este detalle es importante al aprender R, en especial si tenés experiencia en otros lenguajes. Confundir estos sistemas puede llevar a errores difíciles de detectar.

24.2 Matrices

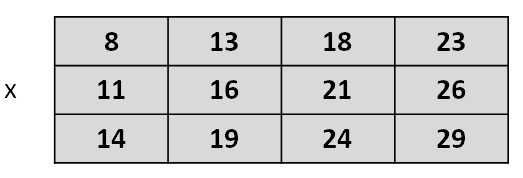
Un arreglo bidimensional representa lo que habitualmente conocemos en matemática como matriz y por eso también lo llamamos de esa forma. Podemos imaginar que en una matriz los elementos están organizados en filas y columnas formando una tabla. Por ejemplo, la siguiente es una matriz llamada x:

Ejemplo de una matriz numérica.

Ejemplo de una matriz numérica.

A diferencia de los vectores, las matrices requieren dos índices para señalar la posición de cada elemento, el primero para indicar la fila y el segundo para indicar la columna. Los mismos se colocan entre corchetes, separados por una coma, al lado del identificador de la matriz. De esta forma, si hablamos de x[1, 3] hacemos referencia a la posición ocupada por el valor 18, mientras que si mencionamos x[3, 1] nos referimos al valor 14.

Ejemplo de una matriz numérica: se usan dos índices para señalar cada posición.

Ejemplo de una matriz numérica: se usan dos índices para señalar cada posición.

Al tamaño de una matriz, es decir, cuántas filas y columnas tiene, se le dice dimensión. La matriz anterior es de dimensión \(3 \times 4\).

Para crear una matriz en R, usamos la función matrix(). Su primer argumento, data, es un vector con todos los elementos que queremos guardar en la matriz. Luego, se indica la cantidad de filas para la misma con nrow o la cantidad de columnas con ncol:

x <- matrix(data = c(8, 11, 14, 13, 16, 19, 18, 21, 24, 23, 26, 29), nrow = 3)
x
     [,1] [,2] [,3] [,4]
[1,]    8   13   18   23
[2,]   11   16   21   26
[3,]   14   19   24   29

El siguiente código es equivalente:

x <- matrix(data = c(8, 11, 14, 13, 16, 19, 18, 21, 24, 23, 26, 29), ncol = 4)

Notar que R ubica a los valores provistos en el vector llenando primero la columna 1, luego la 2, etc. Ese comportamiento puede ser modificado con el argumento byrow, que por default es FALSE. Si lo cambiamos a TRUE los elementos son ubicados por fila. Además, podemos usar saltos de líneas en el código para imaginar mejor el aspecto final de la matriz. Esto no tiene ningún impacto en R, sólo sirve para que el código sea más fácil de leer. Las siguiente sentencia es equivalente a las anteriores:

x <- matrix(c(
              8, 13, 18, 23, 
              11, 16, 21, 26, 
              14, 19, 24, 29
            ), 
            nrow = 3,
            byrow = TRUE)

Si colocamos un único valor como primer argumento en la función matrix(), el mismo se repetirá en todas las posiciones. En este caso sí o sí tenemos que indicar cuántas filas y columnas deseamos:

y <- matrix(0, nrow = 2, ncol = 5)
y
     [,1] [,2] [,3] [,4] [,5]
[1,]    0    0    0    0    0
[2,]    0    0    0    0    0

Tenemos las siguientes funciones para analizar el tamaño de las matrices:

dim(x) # devuelve un vector con la cantidad de filas y columnas
[1] 3 4
nrow(x)
[1] 3
ncol(x)
[1] 4

Podemos recorrer todas las posiciones de una matriz con una estructura iterativa doble: nos situamos en la primera fila y recorremos cada columna, luego en la segunda fila y recorremos todas las columnas y así sucesivamente:

for (i in 1:3) {
  for (j in 1:4) {
    ...hacer algo con x[i, j]...
  }
}

Recorrer todas las posiciones de una matriz fila por fila.

Recorrer todas las posiciones de una matriz fila por fila.

También se puede recorrer la matriz por columna, si modificamos ligeramente las estructuras iterativas:

for (j in 1:4) {
  for (i in 1:3) {
    ...hacer algo con x[i, j]...
  }
}

Recorrer todas las posiciones de una matriz columna por columna.

Recorrer todas las posiciones de una matriz columna por columna.

Se puede usar cualquier letra o palabra como variables iteradoras, pero el uso de i para las filas y de j para las columnas es bastante común.

También podemos asignar valores en cada celda mientras recorremos la matriz. De hecho, la matriz x del ejemplo puede ser generada así, donde los índices i y j no sólo señalan una posición en particular dentro de la matriz, sino que además se usan para hacer el cálculo del valor a asignar:

x <- matrix(0, nrow = 3, ncol = 4)
for (i in 1:nrow(x)) {
    for (j in 1:ncol(x)) {
        x[i, j] <- 3 * i + 5 * j
    }
}
x
     [,1] [,2] [,3] [,4]
[1,]    8   13   18   23
[2,]   11   16   21   26
[3,]   14   19   24   29

Trasponer una matriz

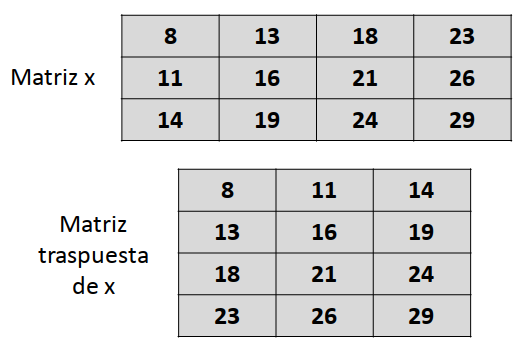
En Álgebra, una matriz traspuesta es una nueva matriz obtenida al intercambiar las filas por las columnas de una matriz original. En otras palabras, la primera fila de la matriz original se convierte en la primera columna de la matriz traspuesta, y así sucesivamente. Si la matriz original es de dimensión \(m \times n\), su matriz transpuesta es de dimensión \(n \times m\):

La matriz x y su traspuesta.

La matriz x y su traspuesta.

Podemos escribir un programa para generar la matriz traspuesta, teniendo en cuenta que cada elemento que originalmente ocupa la posición [i, j] en la matriz original, debe pasar a ocupar la posición [j, i] en la matriz traspuesta:

Dado que en R vamos a asignar valores en la matriz de manera literal, primero la creamos y luego usamos nrow() y ncol() para obtener los correspondientes valores de nf y nc. En el siguiente ejemplo, además, todas las posiciones de la matriz traspuesta son iniciadas con el valor NA.

# Matriz original
x <- matrix(c( 8, 13, 18, 23, 
              11, 16, 21, 26, 
              14, 19, 24, 29), 
            nrow = 3, byrow = TRUE)

# Cantidad de filas y columnas de la original
nf <- nrow(x)
nc <- ncol(x)

# Definimos la traspuesta, inicialmente llena de valores NA
traspuesta <- matrix(NA, nrow = nc, ncol = nf)

# Generamos la matriz traspuesta
for (i in 1:nf) {
    for (j in 1:nc) {
        traspuesta[j, i] <- x[i, j]
    }
}

cat("Matriz original:\n")
x
cat("\nMatriz traspuesta:\n")
traspuesta
Matriz original:
     [,1] [,2] [,3] [,4]
[1,]    8   13   18   23
[2,]   11   16   21   26
[3,]   14   19   24   29

Matriz traspuesta:
     [,1] [,2] [,3]
[1,]    8   11   14
[2,]   13   16   19
[3,]   18   21   24
[4,]   23   26   29

Las matrices no deben confundirse con otras estructuras como los data.frames de R. Un data.frame permite almacenar datos tabulares, es decir, organizados en filas y columnas, de forma similar a una hoja de cálculo o una tabla de base de datos. Aunque las matrices y los data.frames pueden parecer similares porque ambos organizan datos en filas y columnas, existe una diferencia fundamental entre ellos: en una matriz todos los elementos deben ser del mismo tipo (por ejemplo, todos numéricos), mientras que un data.frame puede contener columnas de distintos tipos (por ejemplo, números, texto y otras cosas a la vez). En esta asignatura no trabajaremos con data.frames, ya que no aprendemos sobre análisis o manejo de datos, pero sí lo harán en Laboratorio de Datos 1.

24.3 Atributos

En R, un atributo o attribute es información adicional que se puede asociar a un objeto, como un vector atómico, sin modificar los valores que contiene. Es decir, los atributos actúan como metadatos: datos sobre los datos. Estos no cambian el contenido del objeto, no se muestran cuando lo imprimimos directamente, y no suelen influir en operaciones básicas. Sin embargo, algunas funciones de R pueden utilizar atributos específicos para tratar los objetos de una manera especial.

Podemos averiguar si un objeto tiene atributos con la función attributes(). Si el objeto no tiene ninguno, la función devuelve NULL.

v <- c(10, -9, 9, 1, 7, 2)
attributes(v)
NULL

En este ejemplo, el vector atómico v de tipo numérico no tiene atributos asociados. Aunque un vector atómico común no tiene atributos por defecto, R construye muchas estructuras de datos más complejas, como matrices, otros arrays, factores, fechas, etc.) agregando atributos a vectores simples.

A continuación, veremos algunos atributos fundamentales.

24.3.1 names (nombres)

Uno de los atributos más comunes es el de los names. Se usa para asignar una etiqueta a cada elemento de un vector. Esto puede ayudar a interpretar los datos o acceder a elementos por nombre.

Por ejemplo, en el vector cantidades vamos a anotar cuántas frutas (manzanas, naranjas, bananas y peras) tenemos que comprar:

cantidades <- c(3, 7, 2, 1)
cantidades
[1] 3 7 2 1
names(cantidades)
NULL

Seguramente es más cómodo si usamos el atributo names para anotar ponerle a cada valor un nombre que indique la fruta correspondiente:

names(cantidades) <- c("manzanas", "naranjas", "bananas", "peras")
cantidades
manzanas naranjas  bananas    peras 
       3        7        2        1

El contenido del vector no cambia, pero al imprimirlo ahora se muestran las etiquetas junto a los valores. Estas etiquetas no afectan a las operaciones que queramos hacer:

# Mejor compro 4 manzanas más
cantidades[1] <- cantidades[1] + 4
cantidades
manzanas naranjas  bananas    peras 
       7        7        2        1

Algo muy interesante de tener nombres, es que los podemos usar para indexar:

cantidades[3]
bananas 
      2 
cantidades["bananas"]
bananas 
      2

Podemos eliminar todas las etiquetas asignando NULL al atributo names():

names(cantidades) <- NULL
cantidades
[1] 7 7 2 1

También se pueden nombrar los elementos de un vector directamente cuando lo creamos:

cantidades <- c(manzanas = 3, naranjas = 7, bananas = 2, peras = 1)
cantidades
manzanas naranjas  bananas    peras 
       3        7        2        1

En el caso de las matrices, se le puede asignar nombres a sus filas y columnas. Esto se puede hacer después de crear la matriz

x <- matrix(c( 8, 13, 18, 23, 
              11, 16, 21, 26, 
              14, 19, 24, 29), 
            nrow = 3, byrow = TRUE)
rownames(x) <- c("A", "B", "C")
colnames(x) <- c("grupo1", "grupo2", "grupo3", "grupo4")
x
  grupo1 grupo2 grupo3 grupo4
A      8     13     18     23
B     11     16     21     26
C     14     19     24     29

o al crearla dentro de la función matrix():

x <- matrix(c( 8, 13, 18, 23, 
              11, 16, 21, 26, 
              14, 19, 24, 29), 
            nrow = 3, byrow = TRUE,
            dimnames = list(Categorias = c("A", "B", "C"), 
                            Grupos = c("grupo1", "grupo2", "grupo3", "grupo4")))
x
          Grupos
Categorias grupo1 grupo2 grupo3 grupo4
         A      8     13     18     23
         B     11     16     21     26
         C     14     19     24     29

En este último ejemplo, se han elegido arbitrariamente los nombres Categorias y Grupos para llamar al conjunto completo de las filas y de las columnas, respectivamente. Esos nombres pueden ser cambiados por otros. Además, los nombres fueron encerrados en una lista, una estructura de datos que estudiaremos en los próximos capítulos.

Al igual que con los vectores, podemos usar los nombres de filas y columnas para indexar:

x["B", "grupo2"]
[1] 16

24.3.2 dim (dimensiones)

El atributo dim en R define las dimensiones de un objeto, y permite transformar un vector atómico en una estructura multidimensional, como una matriz o un array. De hecho, una matriz es, en realidad, un vector atómico con un atributo adicional: dim, que define sus dimensiones. Por ejemplo, para crear una matriz de 3 filas y 2 columnas a partir de un vector de longitud 6, basta con asignar el atributo correspondiente:

# Creamos un vector atómico numérico
x <- c(8, 11, 14, 13, 16, 19, 18, 21, 24, 23, 26, 29)
x
 [1]  8 11 14 13 16 19 18 21 24 23 26 29
length(x)
[1] 12
typeof(x)
[1] "double"
is.vector(x)
[1] TRUE
is.matrix(x)
[1] FALSE
dim(x)
NULL
# Una matriz es un vector al que se le asigna un atributo "dim"
dim(x) <- c(3, 4)
x
     [,1] [,2] [,3] [,4]
[1,]    8   13   18   23
[2,]   11   16   21   26
[3,]   14   19   24   29
length(x)
[1] 12
typeof(x)
[1] "double"
is.vector(x)
[1] FALSE
is.matrix(x)
[1] TRUE
dim(x)
[1] 3 4

Al asignar dim, R reorganiza internamente los datos del vector sin modificar sus valores, pero cambia su forma y la manera en que se imprimen o manipulan. Lo anterior nos enseña que para crear una matriz podemos usar la función matrix() como vimos antes, o agregarle un atributo dim a un vector. Podemos cambiar el atributo dim para organizar los valores en otra disposición:

dim(x) <- c(2, 6)
x
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    8   14   16   18   24   26
[2,]   11   13   19   21   23   29

24.3.3 class (clase)

El atributo class indica de qué clase es un objeto y esto le sirve a R para saber cómo debe comportarse y qué métodos (funciones) deben aplicarse sobre él. Dependiendo de la clase de objeto, R hace algo distinto al imprimirlo, al indexarlo o al aplicar funciones.

A continuación, tomamos la matriz x del ejemplo anterior. Vemos que es una estructura de datos numérica, ya que así lo indica typeof(). Pero además, vemos que no es un vector atómico numérico común y corriente, sino que se trata de una matriz, como indica class(). Los objetos de clase matrix tienen particularidades propias, como el atributo dim que indica en cuántas filas y columnas se organiza su contenido.

x
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    8   14   16   18   24   26
[2,]   11   13   19   21   23   29
typeof(x)
[1] "double"
class(x)
[1] "matrix" "array"

Cualquier lenguaje permite crear nuevas clases a partir de objetos más simples. Los objetos pertenecientes a una determinada clase tiene sus propios atributos, particularidades y formas de funcionar. Muchas funciones en R se comportan de forma distinta dependiendo de la clase de un objeto.