14 Creación de nuevas funciones en R

En este capítulo analizaremos por qué el uso de funciones es una herramienta poderosa en la resolución de problemas y cómo nos permite estructurar mejor nuestro código mediante la descomposición algorítmica. Luego, aprenderemos cómo definir funciones en R, especificando parámetros con valores por defecto y controlando su comportamiento.

14.1 La importancia de la descomposición algorítmica

Un principio clave en la resolución de problemas es la descomposición algorítmica, es decir, dividir un problema complejo en partes más pequeñas y manejables. En programación, esto se traduce en la creación de subalgoritmos: fragmentos de código que resuelven una parte específica del problema. Este enfoque, también conocido como descomposición modular, facilita la comprensión del código y permite reutilizar soluciones ya escritas.

En R, los subalgoritmos se implementan a través de funciones. Una función encapsula una serie de instrucciones y puede ser invocada desde distintos puntos del código cada vez que se necesite, sin necesidad de reescribir esas instrucciones encapsuladas una y otra vez. Esto aporta varios beneficios fundamentales:

Mejor legibilidad del código: si el programa es muy largo porque las mismas instrucciones aparecen muchas veces, encerrarlas dentro de una función que es invocada en una sola línea cada vez que se necesita hace que el código se vuelva más corto. Además, al dar a una función un nombre descriptivo, el propósito de la línea de código que la invoca se vuelve más claro. Todo esto resulta en código más comprensible para las personas.
Facilidad de mantenimiento: si hay que modificar una funcionalidad, basta con actualizar la función sólo en el lugar donde está definida, en lugar de hacerlo en múltiples fragmentos de código copiados y pegados.
Reducción de errores: copiar y pegar código manualmente puede dar lugar a errores accidentales, como olvidar cambiar un nombre de variable en alguna de las copias.
Mayor eficiencia y reutilización: una vez definida, una función puede utilizarse muchas veces, en el mismo o en otros proyectos, ahorrando tiempo y esfuerzo.

Las funciones son fundamentales para organizar y estructurar programas, ya que permiten dividir un problema en partes más pequeñas y reutilizar código en diferentes puntos del programa sin necesidad de repetirlo.

14.2 Definición de una función

En R, una función es un bloque de código reutilizable que realiza una tarea específica. Las funciones toman argumentos de entrada, ejecutan una serie de instrucciones y pueden devolver un resultado.

Para ejemplificar, podemos decir que la noción de función en programación se asemeja a la idea matemática de función de una o más variables. Pensemos en la función \(f(x, y) = x^2 + 3y\) (ejemplo 1). Si queremos saber cuál es el valor numérico de la función \(f\) cuando \(x\) toma el valor \(4\) e \(y\) toma el valor \(5\), reemplazamos en la expresión anterior las variables por los valores mencionados y obtenemos: \(f(4, 5) = 4^2 + 3 \times 5 = 31\).

Podemos definir dicha función en R de la siguiente manera:

f <- function(x, y) {
    resultado <- x^2 + 3 * y
    return(resultado)
}

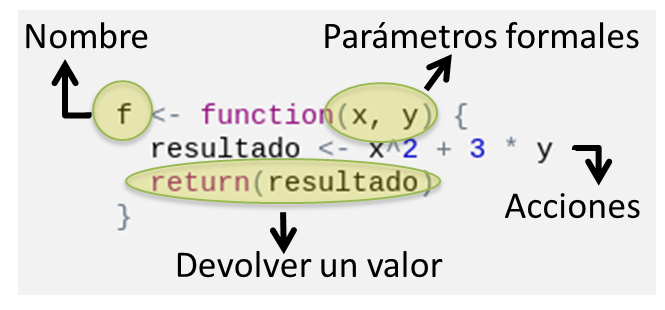
La estructura general de la definición de una función consta de tres componentes:

nombre <- function(argumentos) {
  cuerpo
}

Nombre: elegido por nosotros, respetando las reglas para la elección de nombres para objetos y buscando que provea una buena descripción del propósito de la función. Usamos el operador de asignación (<-) para asociar ese nombre a la definición de la función, señalada con la palabra clave function.
Argumentos o parámetros: listado de piezas de información que la función necesita para operar y que pueden variar cada vez que es invocada. Se listan entre paréntesis y separados por comas, a la derecha de la palabra clave function.
Cuerpo: conjunto de instrucciones de programación que la función ejecuta cada vez que es invocada, encerrado por un par de llaves. Generalmente finaliza con la función return(), que indica el fin de la ejecución y provee el objeto que la función devuelve.

Figura 14.1: Estructura de una función en R.

Una vez que la definición de la función es ejecutada, pasa a formar parte de los objetos que conforman al ambiente global, como se puede apreciar al verla listada en el panel Environment de RStudio. A partir de este momento, podemos utilizarla, como parte de otro programa. Para invocarla, escribimos el nombre de la función y entre paréntesis los valores que nos interesan para el cálculo:

# Ejemplos de uso de la función f
f(4, 5)

[1] 31

f(6, -5)

[1] 21

f(0, 0)

[1] 0

Los parámetros o argumentos constituyen el input o información de entrada con la cual se realizarán las operaciones. Considerando el ejemplo, decimos que \(x\) e \(y\) son los parámetros formales o ficticios, ya que son símbolos que permiten expresar de manera general las acciones que la función ejecuta. Describen lo que uno diría en palabras: “hay que tomar a \(x\), elevarlo al cuadrado y sumarle la \(y\) multiplicada por 3”.

Los valores en los cuales se quiere evaluar la función se llaman parámetros actuales o reales. Por ejemplo, si nos interesa calcular \(f(4, 5)\), los valores \(4\) y \(5\) son los parámetros actuales y se establece una correspondencia entre el parámetro formal \(x\) y el actual \(4\), así como entre la \(y\) y el \(5\). El resultado que se obtiene, como observamos antes, es \(31\) y este es el valor que la función devuelve.

Recordando lo discutido en Sección 2.6, podemos apreciar que los siguientes usos de la función f() son equivalentes:

f(4, 5)

[1] 31

f(x = 4, y = 5)

[1] 31

f(y = 5, x = 4)

[1] 31

Sin embargo, no son equivalentes los siguientes:

# Siguiendo el orden de definición, x recibe el valor 4 e y recibe el 5:
f(4, 5)

[1] 31

# Siguiendo el orden de definición, x recibe el valor 5 e y recibe el 4:
f(5, 4)

[1] 37

A continuación, podemos ver casos que generan error por hacer un uso incorrecto de la función:

# Error por omitir un argumento de uso obligatorio (x recibe 4, falta y)
f(4)

Error in f(4): argument "y" is missing, with no default

# Error por proveer más argumentos de los declarados en la definición
f(4, 5, 6)

Error in f(4, 5, 6): unused argument (6)

14.3 Función `return()`

La instrucción return() provoca la inmediata finalización de la ejecución de la función e indica cuál es el objeto que la misma devuelve como resultado. Aunque generalmente lo encontramos al final de la definición de la función, es posible incluir más de un return() para que el resultado dependa de alguna condición, aunque sólo uno llegue a ejecutarse.

Uso de dos instrucciones return() en la definición de una función que devuelve cuál es el mayor entre dos números:

maximo <- function(num1, num2) {
    if (num1 > num2) {
        return(num1)
    } else {
        return(num2)
    }
}

maximo(0, 10)

[1] 10

maximo(0, -10)

[1] 0

La función return() puede omitirse, ya que si no está presente se devuelve el resultado de la última expresión analizada. Por eso, las siguientes funciones son equivalentes:

# return explícito
sumar1 <- function(x, y) {
    resultado <- x + y
    return(resultado)
}

# return implícito
sumar2 <- function(x, y) {
    x + y
}

sumar1(4, 5)

[1] 9

sumar2(4, 5)

[1] 9

No obstante, es aconsejable usar return() para evitar ambigüedades y ganar en claridad. Además, en funciones más complejas, su uso puede ser indispensable para indicar el término de la evaluación de la función.

14.4 Argumentos con valores asignados por defecto

Hemos visto que algunos argumentos de las funciones predefinidas de R tienen valores asignados por defecto, como es el caso de la función log(), que a menos que indiquemos otra cosa opera con la base natural. Cuando definimos nuestras propias funciones, también es posible asignarle un valor por defecto a uno o más de sus argumentos.

Recordemos la definición de la función f:

f <- function(x, y) {
    resultado <- x^2 + 3 * y
    return(resultado)
}

Esta función también podría ser definida así:

nueva_f <- function(x, y = 100) {
    resultado <- x^2 + 3 * y
    return(resultado)
}

Esto significa que si no proveemos un valor para el argumento y, se le asignará por default el valor 100. Luego:

nueva_f(4)

[1] 316

En el caso anterior se hace corresponder el 4 al primer argumento de la función, x, y como no proveemos ningún otro parámetro actual, y recibe por defecto el valor 100 y se calcula: x^2 + 3 * y = 16 + 300 = 316.

Por supuesto, podemos proveer cualquier otro valor para y, de modo que no se use el valor asignado por default:

nueva_f(4, 5)

[1] 31

Como x no tiene valor asignado por default en la función nueva_f(), siempre debemos pasarle uno. En caso contrario, recibiremos un error:

nueva_f(y = 5)

Error in nueva_f(y = 5): argument "x" is missing, with no default

nueva_f()

Error in nueva_f(): argument "x" is missing, with no default

14.5 ¿Dónde escribimos el código que define nuestras funciones?

El código que define una función tiene que ser ejecutado antes que el código que pretende usarla, de modo que la función aparezca entre los objetos disponibles del Global Environment. No podemos usar una función cuya definición no haya sido ejecutada, puesto que produciremos un error que indica que tal objeto no existe. Esto nos obliga a pensar dónde escribimos el código para crear nuevas funciones y en qué momento es ejecutado.

En proyectos de pequeña extensión, donde todo el problema se resuelve en un único y acotado script y sólo se definen unas pocas nuevas funciones, podemos incluirlas al comienzo del archivo, para que sean evaluadas antes del código que las invoca.

A continuación se presenta el contenido de un breve script de código que comienza con la definición de dos funciones, usadas posteriormente.

# ---------------------------------------------------------------
# DEFINICIÓN DE FUNCIONES
# ---------------------------------------------------------------

f <- function(x, y) {
    resultado <- x^2 + 3 * y
    return(resultado)
}

maximo <- function(num1, num2) {
    if (num1 > num2) {
        return(num1)
    } else {
        return(num2)
    }
}

# ---------------------------------------------------------------
# PROGRAMA
# ---------------------------------------------------------------

rtdo1 <- f(2, 5)
rtdo2 <- f(3, 10)
rtdo3 <- maximo(rtdo1, rtdo2) + 20
cat("El resultado es", rtdo3)

¿Cuál es el mensaje que emite la última línea del script del ejemplo?

Cuanto más grande o complejo es el problema a resolver, más funciones deben ser programadas. Por eso, con el objetivo de tener un mayor orden en nuestro código, podemos escribir nuestras funciones en uno o más archivos separados, creados específicamente para esto (“scripts de funciones”). Si lo hacemos, al comienzo del script en el que estamos resolviendo un problema que involucra el uso de las funciones creadas, debemos incluir una instrucción para que el script de funciones sea evaluado, de modo que las funciones ahí definidas sean ejecutadas y pasen a formar parte del Global Environment. Esta instrucción es la función source(), que toma como único argumento el nombre del script de funciones.

Para ilustrar esto, vamos a recordar que en el ejercicio 6 de la Práctica 2 escribimos un programa para el cálculo de factoriales. Dado que los mismos son muy útiles en variadas aplicaciones, podemos definir una nueva función se encargue de obtenerlos. Escribimos la definición en un script llamado funciones.R, cuyo contenido es:

fact <- function(n) {
    resultado <- 1
    if (n > 0) {
        for (i in 1:n) {
            resultado <- resultado * i
        }
    }
    return(resultado)
}

Luego, en cualquier script donde se presente un problema que requiera el cálculo de factoriales, vamos a pedirle a R que ejecute el código guardado en funciones.R con la sentencia source(), como paso inicial. Por ejemplo, en el script mis_factoriales.R se usa la función fact() para calcular el factorial de los primeros diez números naturales. Su contenido es:

# ---------------------------------------------------------------
# PROGRAMA: Mostrar los factoriales de los 10 primeros naturales
# ---------------------------------------------------------------

source("funciones.R")

for (j in 1:10) {
    cat("El factorial de", j, "es igual a", fact(j), "\n")
}

El factorial de 1 es igual a 1 
El factorial de 2 es igual a 2 
El factorial de 3 es igual a 6 
El factorial de 4 es igual a 24 
El factorial de 5 es igual a 120 
El factorial de 6 es igual a 720 
El factorial de 7 es igual a 5040 
El factorial de 8 es igual a 40320 
El factorial de 9 es igual a 362880 
El factorial de 10 es igual a 3628800

Gracias a source() todas las funciones definidas en el archivo funciones.R aparecerán en el entorno y no hay necesidad ni siquiera de abrirlo. Esto funcionará siempre que este archivo esté guardado en el directorio de trabajo. En caso contrario, se debe indicar en source() el path completo hacia el script de funciones (por ejemplo, C:/Documentos/Facultad/funciones.R), pero esto no es recomendable. Es preferible que todos los archivos estén correctamente organizados en la carpeta principal de nuestro proyecto y, en caso de necesitarlo, usemos rutas relativas con respecto a la misma, tal como mencionamos en Sección 5.3.

Más adelante veremos una forma mejor de guardar y distribuir las funciones que inventamos: podemos crear un nuevo paquete de R que las almacene.

14.1 La importancia de la descomposición algorítmica

14.2 Definición de una función

14.3 Función return()

14.4 Argumentos con valores asignados por defecto

14.5 ¿Dónde escribimos el código que define nuestras funciones?

14.3 Función `return()`