f <- function(a = 10) {
a <- (a - 10) * (a + 10)
return(a)
}
g <- function(x, y) {
b <- x - y * 2
c <- b * f(b)
d <- f() - c
return(d)
}
a <- 6
b <- 1
g(a, b)Práctica de la Unidad 3
Instrucciones generales para resolver los problemas de esta práctica:
- Abrir RStudio y crear un nuevo proyecto llamado
unidad3, para guardar allí todos los archivos que usaremos. Asegurarse de que RStudio esté trabajando con este proyecto abierto. - Al comenzar a resolver cada ejercicio:
- Eliminar todos los objetos del Global Environment, para evitar confusiones con objetos que hayan sido creados para resolver otro problema.
- Crear y guardar en la carpeta del proyecto un nuevo script con el nombre
ejercicio_*.Rpara almacenar de manera organizada la solución de cada problema (por ejemplo,ejercicio_01.R,ejercicio_02.R, etc.) - A menos que se indique lo contrario, utilizar cada uno de estos scripts para escribir el código que crea la función pedida en el ejercicio y también el código con ejemplos para usarla.
Ejercicio 1
Definir una nueva función
f1(x1, x2, x3)que calcule y devuelva la siguiente expresión matemática:\[ \frac{x_1}{x_2} + x_3^2 + x_2 * x_3 \]
Ejemplo de su uso:
> f1(5, 2, 3) [1] 17.5Modificar el código de
f1para crear una funciónf2(x1, x2, x3)que realiza el mismo cálculo, pero asumiendo que los argumentosx2yx3son opcionales. Si el usuario de la función no provee un valor para ellos, deben tomar el valor1. Chequear que el resultado coincide con los siguientes ejemplos y analizar por qué se originan:> f2(5, 2, 3) [1] 17.5 > f2(5) [1] 7 > f2(5, 2) [1] 5.5 > f2(5, x3 = 3) [1] 17 > f2(x2 = 2, x3 = 3) Error in f2(x2 = 2, x3 = 3) : argument "x1" is missing, with no defaultModificar el código de
f2para crear una funciónf3(x1, x2, x3)que realiza el mismo cálculo, con los mismos valores por defecto parax2yx3, pero que devuelve-100si alguno de los argumentos es un valor negativo. Ejemplos de su uso:> f3(5, 2, 3) [1] 17.5 > f3(-5, 2, 3) [1] -100 > f3(-5) [1] -100 > f3(5, x3 = -3) [1] -100
Ejercicio 2
Dados dos números enteros a y b que pueden ser negativos o positivos, crear una función llamada suma_secuencia(a, b) para calcular la suma de todos los números enteros entre a y b, incluyéndolos. Si estos números son iguales, la función debe devolver el valor que comparten. Ejemplos de su uso:
> suma_secuencia(1, 3)
[1] 6
> suma_secuencia(30, 40)
[1] 385
> suma_secuencia(5, 2)
[1] 14
> suma_secuencia(-2, 3)
[1] 3
> suma_secuencia(-7, -5)
[1] -18
> suma_secuencia(-3, -3)
[1] -3
> suma_secuencia(3, 3)
[1] 3
> suma_secuencia(-3, -5)
[1] -12Ejercicio 3
Escribir un programa en R para la creación de la función triangulos(a, b, c) que a partir de la longitud de los tres lados de un triángulo a, b y c (valores positivos) lo clasifica con los siguientes resultados posibles:
- No forman un triángulo (un lado mayor que la suma de los otros dos).
- Triángulo equilátero (tres lados iguales).
- Triángulo isósceles (dos lados iguales).
- Triángulo escaleno (tres lados distintos).
Como resultado, la función devuelve uno de estos valores de tipo carácter, según corresponda: “no es triángulo”, “equilátero”, “isósceles” o “escaleno”.
Ejemplos de uso:
triangulos(2, 3, 4)
[1] "escaleno"
triangulos(2, 3, 10)
[1] "no es triángulo" Ejercicio 4
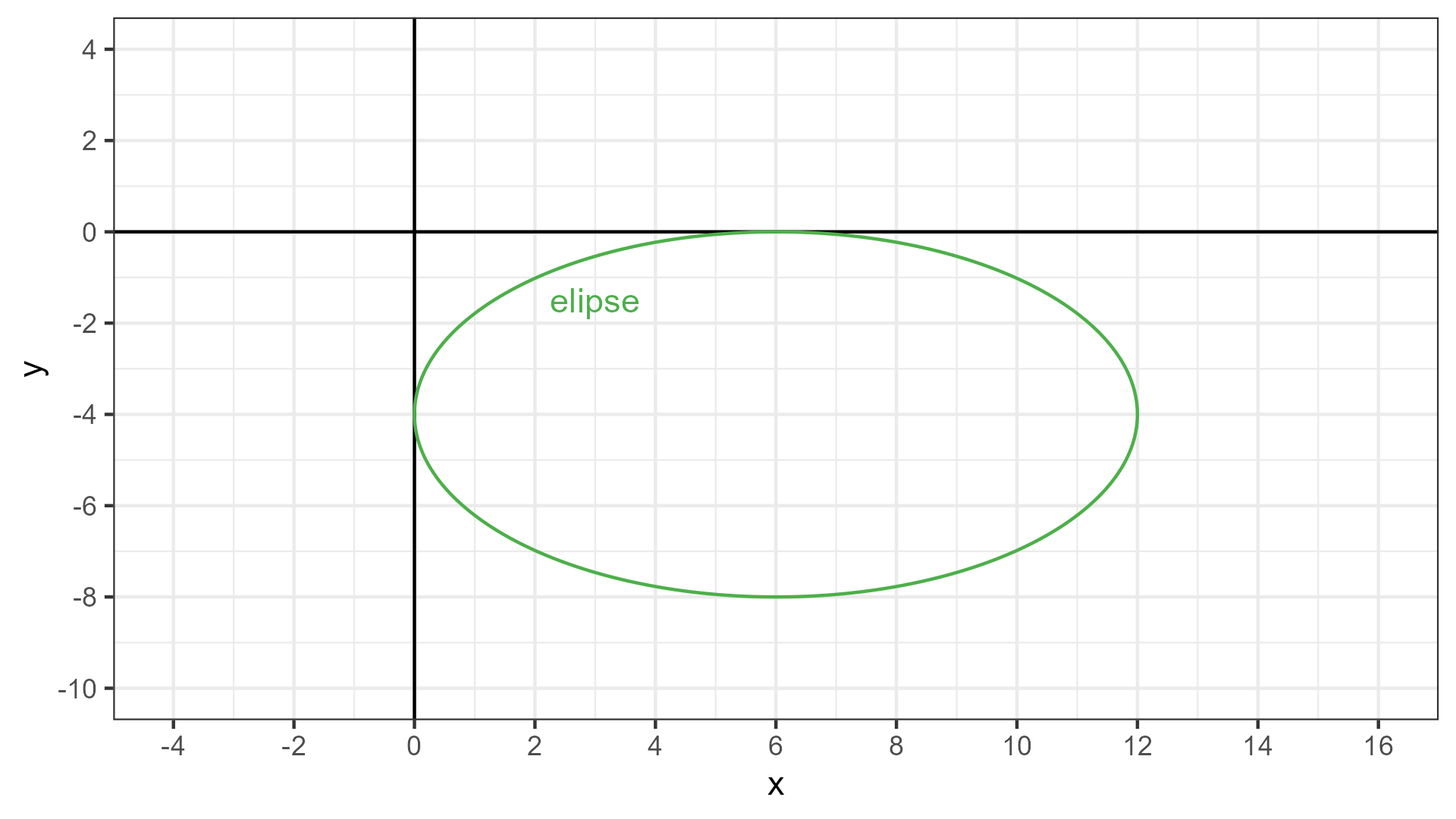
Escribir un programa en R para la creación de la función elipse(x, y) que permite determinar si un punto de coordenadas \((x, y)\) está dentro o no de la elipse definida por la ecuación:
\[\frac{(x - 6) ^ 2}{36} + \frac{(y + 4) ^ 2}{16} = 1\]
Si el punto está contenido en la elipse, la función devuelve el valor lógico TRUE y en caso contrario, FALSE. En caso de que sea invocada sin valores para los argumentos x e y, la función realiza la misma evaluación pero para el origen, es decir, para el punto \((0, 0)\).
Observación: si un punto se encuentra exactamente sobre la curva definida por la elipse, la fórmula anterior evaluada en las coordenadas \((x, y)\) del punto es exactamente igual a 1. Si el punto está dentro de la elipse, da menor que 1. Si está fuera, da mayor que 1. A continuación se presenta la representación gráfica de la elipse en cuestión:
Ejemplos del uso de la función:
elipse(3, 7)
[1] FALSE
elipse(6, -4)
[1] TRUE
elipse()
[1] FALSEEjercicio 5
Imaginemos que con los números impares podemos crear una pirámide como la que se muestra a continuación:
1
3 5
7 9 11
13 15 17 19
21 23 25 27 29Una pirámide puede tener cualquier cantidad de líneas. Definir una función llamada suma_piramide(n) que calcule la suma de los números impares en alguna la fila número n. Por ejemplo:
> suma_piramide(1)
[1] 1
> suma_piramide(2)
[1] 8
> suma_piramide(3)
[1] 27
# Evaluamos la suma de cada una de las primeras 10 filas
for (n in 1:10) {
suma <- suma_piramide(n)
cat("Los impares de la fila", n, "suman", suma, "\n")
}
Los impares de la fila 1 suman 1
Los impares de la fila 2 suman 8
Los impares de la fila 3 suman 27
Los impares de la fila 4 suman 64
Los impares de la fila 5 suman 125
Los impares de la fila 6 suman 216
Los impares de la fila 7 suman 343
Los impares de la fila 8 suman 512
Los impares de la fila 9 suman 729
Los impares de la fila 10 suman 1000 Ejercicio 6
Sin utilizar la computadora, indique cuál es el valor devuelto por
g(a, b)luego de que este programa sea evaluado:Sin utilizar la computadora, indique cuál es el valor de
zque se muestra el algoritmo y explique por qué se indica que la última línea produce un error:f1 <- function(a, b) { x <- a + b y <- x + 2 return(y) } f2 <- function(x) { return(x^2) } # PROGRAMA: Ejemplo de ámbito de las variables x <- 3 y <- 5 a <- f1(x, y) z <- x + f2(a) print(z) print(a + b) # esta línea produce un errorSin usar la computadora, indique cuál es el resultado de evaluar
a + b + c + den la última línea del siguiente código:f = function(x, y = 5, z = x + y) { u = z - x - y return(u) } a = f(10) b = f(10, 10) c = f(10, 10, 10) d = f(10, z = 10) a + b + c + d
Ejercicio 7
Escribir un programa en R para la creación de la función resolvente(a, b, c) que muestra las soluciones de la ecuación de segundo grado \(a x^2 + b x + c = 0\), empleando la fórmula resolvente:
\[x_{1, 2} = \frac{-b \pm \sqrt{(b^2 - 4ac)}}{2a}\]
Observaciones:
- El programa debe emitir mensajes aclaratorios si hay una solución real doble o dos soluciones complejas (en este caso, no las calcula).
- La función escribe en pantalla las soluciones de la ecuación y no es necesario que devuelva ningún objeto en particular.
- Para calcular una raíz cuadrada, podemos usar la función
sqrt(). - Si
aes igual a cero, usar la funciónstop()para devolver un error informativo.
Ejemplos de uso:
> resolvente(1, -1, -2)
Hay dos soluciones reales -1 y 2
> resolvente(1, 2, 1)
Hay una solución real doble: -1
> resolvente(1, 1, 1)
Las soluciones son complejas.
> resolvente(0, 1, 1)
Error in resolvente(0, 1, 1) : (a) debe ser distinto de ceroEjercicio 8
Escribir un programa en R para la creación de la función es_primo(n) que devuelve el valor lógico TRUE si el natural n es un número primo o FALSE en caso contrario. Recordar la siguiente definición:
Un número primo es un número natural mayor que 1, que tiene únicamente dos divisores positivos distintos: él mismo y el 1.
Si el argumento de entrada no es un natural mayor que 1, la función debe imprimir un warning y devolver FALSE como en estos ejemplos:
> es_primo(47)
[1] TRUE
> es_primo(253)
[1] FALSE
> es_primo(2)
[1] TRUE
> es_primo(7.18)
[1] FALSE
Warning message:
In es_primo(7.18) : (n) no es entero
> es_primo(0)
[1] FALSE
Warning message:
In es_primo(0) : (n) no es mayor que 1Ejercicio 9
Escribir un programa en R para la creación de la función cociente(dividendo, divisor) que permite obtener cociente entero y resto en la división de dos números naturales (llamados dividendo y divisor) empleando únicamente operaciones aritméticas de suma y resta. La función escribe un mensaje en pantalla con los valores del dividendo, divisor, cociente y resto, mientras que devuelve el valor del cociente.
Ejemplos de su uso:
cociente(1253, 4)
Dividendo: 1253 # mensajes escritos
Divisor: 4
Cociente: 313
Resto: 1
[1] 313 # valor devuelto
cociente(3, 4)
Dividendo: 3 # mensajes escritos
Divisor: 4
Cociente: 0
Resto: 3
[1] 0 # valor devueltoEjercicio 10
Escribir un programa en R para la creación de la función max_com_div(a, b) que permite calcular el máximo común divisor (mcd) de los números naturales a y b, empleando el algoritmo de Euclides, que propone:
- Dividir al mayor por el menor.
- Si el resto es cero, el divisor es el máximo común divisor.
- Si el resto no es cero, dividir el divisor por el resto.
- Evaluar el nuevo resto de la misma forma y repetir hasta hallar un resto igual a cero. Cuando esto ocurre, el último divisor es el mcd.
Ejemplos de uso:
max_com_div(100, 24)
4
max_com_div(25, 100)
25
max_com_div(24, 24)
24Ejercicio 11
Descargar el archivo
funciones_unidad3.Ren el que se encuentra ya definida la funciónfact()tal como se presentó en Documentación de las funciones. Guardar este archivo en la carpeta del proyecto de esta unidad.Agregar en ese script código para crear una nueva función
combinatorio(m, n)que calcula el número combinatoriomtomado de an(también llamado coeficiente binomial), siendo estos números naturales tales quem >= n. La funcióncombinatorio()debe invocar a la funciónfact()ya provista, teniendo en cuenta que un número combinatorio se define como:\[ C(m, n) = {m \choose n} = \frac{m!}{(m-n)!n!} \]
Crear otro script llamado
ejercicio_11.R, en el cual escribiremos ejemplos de uso de la funcióncombinatorio(m, n). En primera instancia, incluir en este script la sentenciasource(funciones_unidad3.R)para que el contenido del script de funciones sea ejecutado y las mismas sean creadas en el ambiente global. Luego, utilizar la funcióncombinatorio(m, n)para ejemplificar las siguientes propiedades de los números combinatorios:- \({m \choose 0} = 1\)
- \({m \choose m} = 1\)
- \({m \choose 1} = m\)
- \({m \choose n} = {m \choose m - n}\)
- \({m \choose n} = {m - 1 \choose n - 1} + {m - 1 \choose n}\)
Es importante recordar que los números combinatorios sólo están definidos para
m >= n. Probar qué ocurre pasando un valor denmayor quem.El número combinatorio
mtomado de ancon reposición se define como:\[ \bar{C}(m, n) = {m + n - 1 \choose n} = \frac{(m+n-1)!}{(m-1)!n!} \]
En base a lo realizado anteriormente, crear la función
combinatorio2(m, n, r)para generalizar el cálculo de números combinatorios, siendorun argumento adicional que toma el valor lógicoTRUEsi el cálculo es con reposición, yFALSEen caso contrario.Consideraciones:
- Usar la función
combinatorio(m, n)para implementar esta nueva función. - Por defecto, la función debe hacer el cálculo del número combinatorio sin reposición.
- Para
m = 5yn = 2, pruebe si el número de combinaciones posibles es mayor con o sin resposición.
- Usar la función
Ejercicio 12
Escribir la documentación de cada una de las funciones creadas en esta unidad, siguiendo el formato Roxygen.