3 - Algoritmos de ordenamiento
Introducción
Ordenar significa reorganizar un conjunto de elementos según algún criterio, por ejemplo, de menor a mayor, alfabéticamente o por fecha.
Ordenar es una de las tareas más importantes y estudiadas en informática. Almacenar un conjunto de datos de manera ordenada permite realizar búsquedas y otras operaciones de forma más eficiente. Muchos algoritmos avanzados dependen del ordenamiento como parte de su funcionamiento interno.
Python incluye funciones y métodos para ordenar que ya están muy optimizados y, salvo raras excepciones, siempre deberíamos utilizar estas implementaciones. Pero sigue siendo fundamental comprender cómo funcionan los algoritmos detrás de esas operaciones.
Por ejemplo, en el trabajo práctico grupal se usaron dos funciones de ordenamiento, con tiempos de ejecución notablemente distintos. ¿Qué podría explicar semejante diferencia en el desempeño de los algoritmos utilizados? ¿Cuál es la complejidad temporal de cada uno de ellos? ¿Siempre es mejor uno que el otro?
Como veremos en este apunte, existe una gran variedad de algoritmos de ordenamiento, que realizan diferentes operaciones y se basan en distintas estrategias con un mismo objetivo: obtener una secuencia de valores ordenados.
Bubble sort
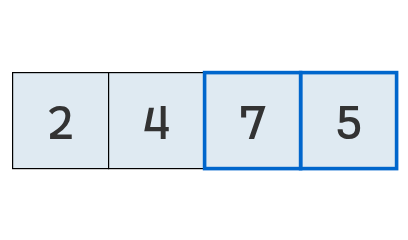
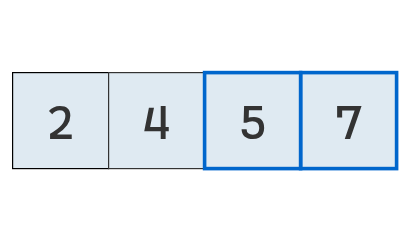
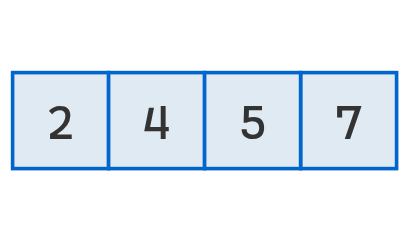
Supongamos que tenemos un arreglo de valores numéricos sin ningún orden particular.
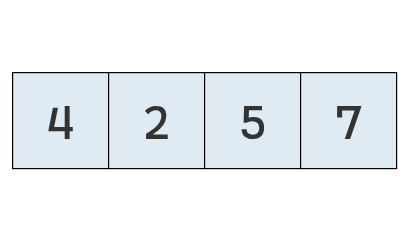
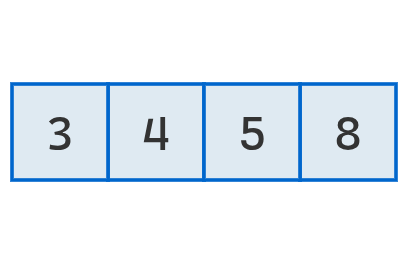
A simple vista, podemos determinar que el arreglo ordenado sería [2, 4, 5, 7].
Sin embargo, para que una computadora llegue al mismo resultado, necesitamos un algoritmo: una secuencia de pasos que garantice que, al ejecutarse, la lista quede ordenada.
En una lista ordenada, cada elemento está seguido por uno mayor o igual. Más formalmente, si tenemos una secuencia \(\boldsymbol{S} = [s_1, s_2, \dots, s_n]\), diremos que está ordenada si se cumple que \(s_i \le s_{i + 1}\) para todo \(i \in \{1, 2, \dots, n - 1\}\).
Por ejemplo, la siguiente lista está ordenada:
[10, 14, 99, 99, 1000]mientras que esta no:
[50, 60, 10, 214]En el primer caso, cada elemento tiene a su derecha un valor mayor o igual; en el segundo, el valor 60 tiene a su derecha un número menor (10), lo que rompe el orden.
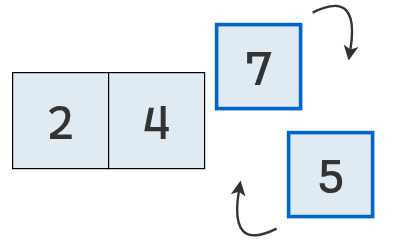
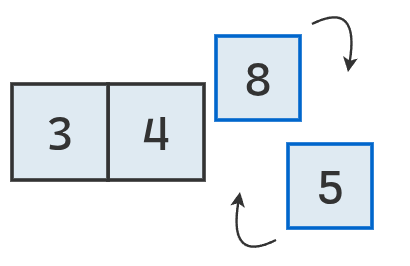
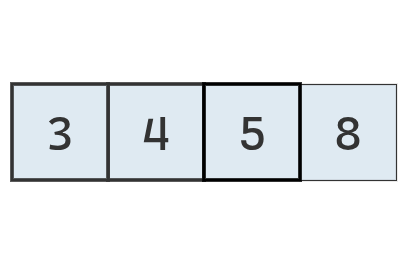
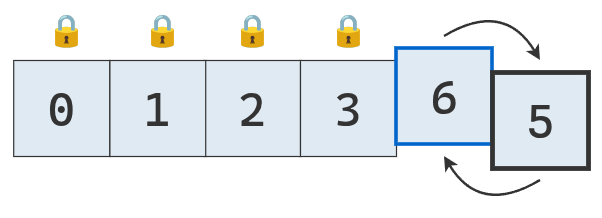
Una forma sencilla de obtener un algoritmo de ordenamiento consiste en comparar cada valor con el siguiente. Si el siguiente es menor, se intercambian; si no, se mantienen en su lugar. El procedimiento continúa con el elemento siguiente, repitiéndose hasta llegar al final de la lista.
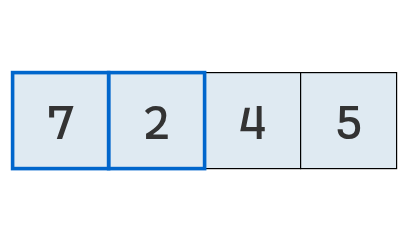
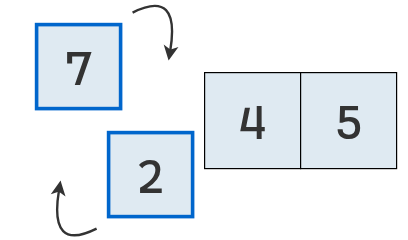
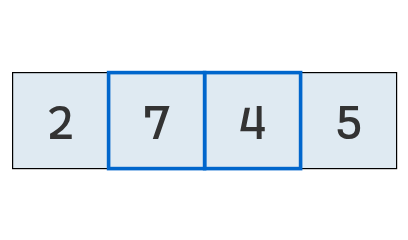
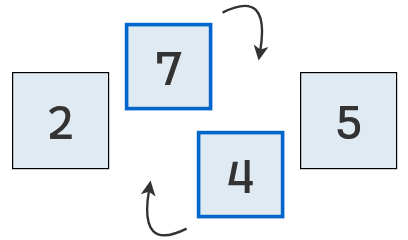
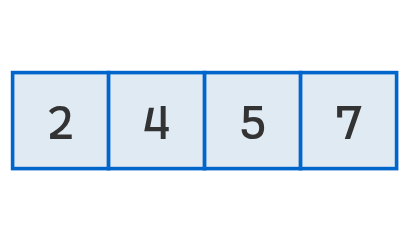
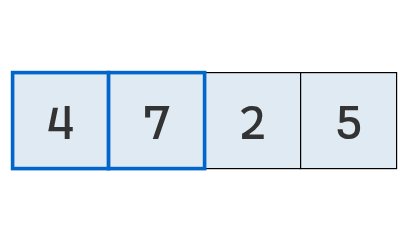
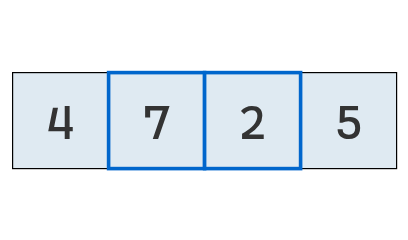
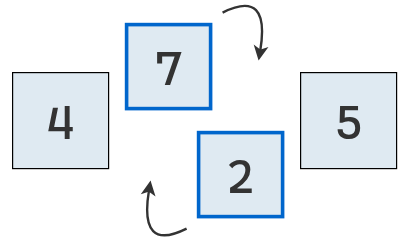
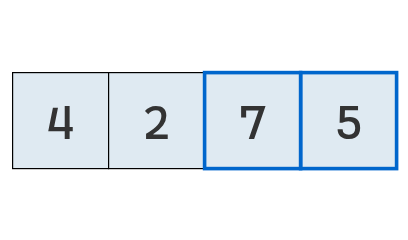
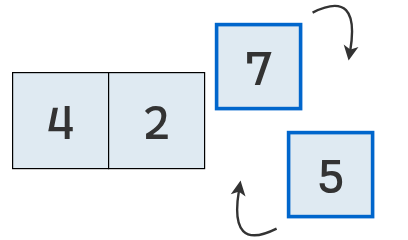
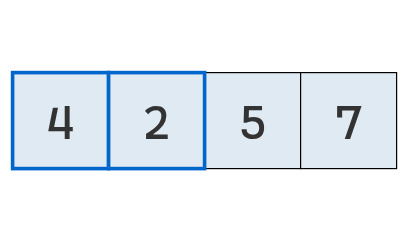
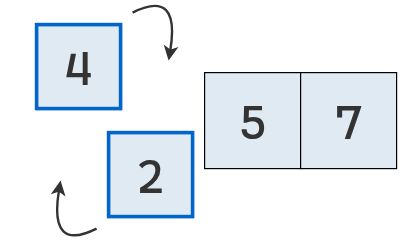
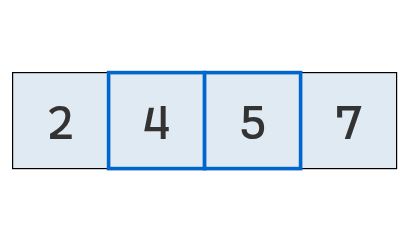
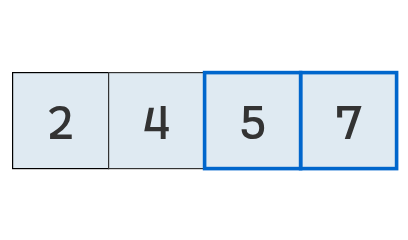
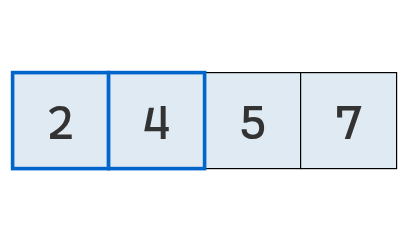
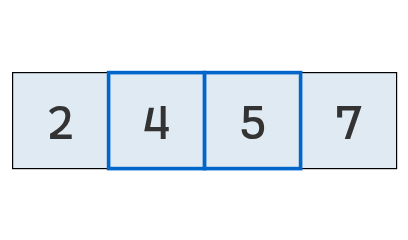
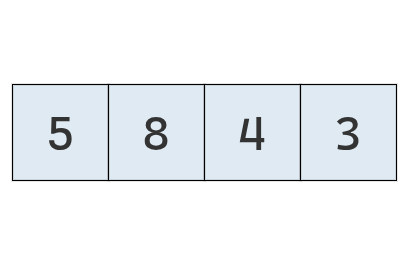
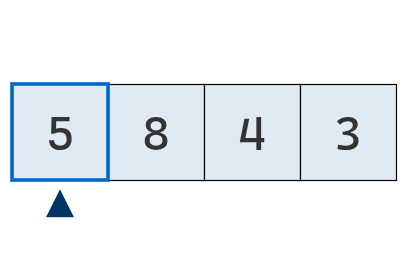
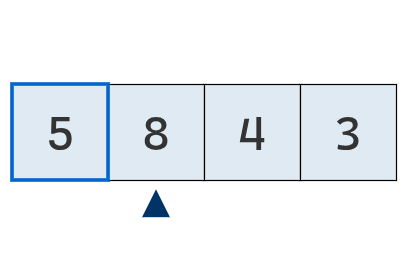
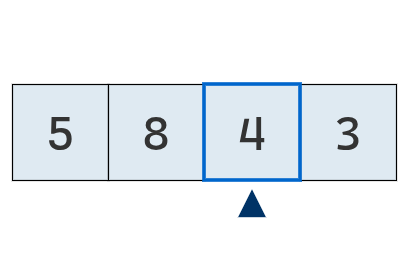
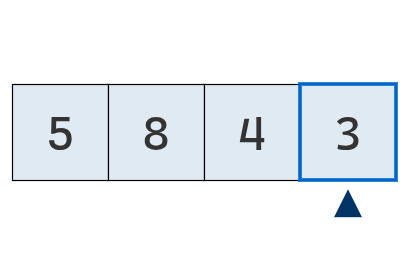
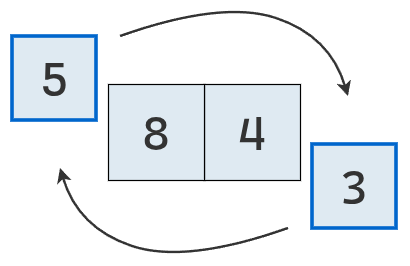
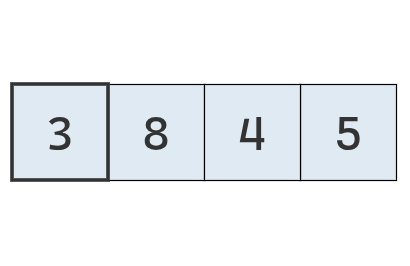
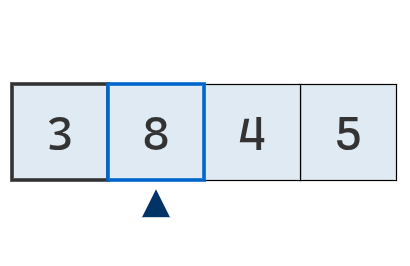
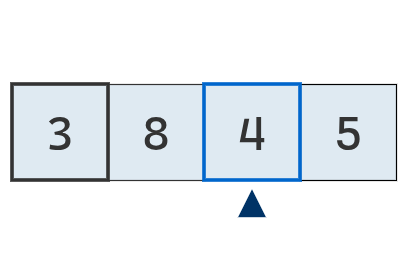
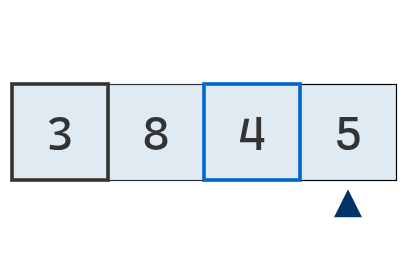
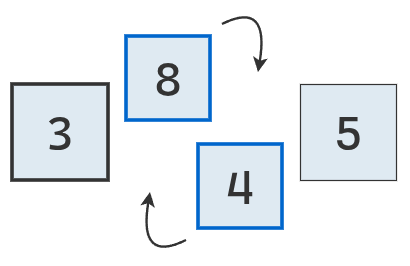
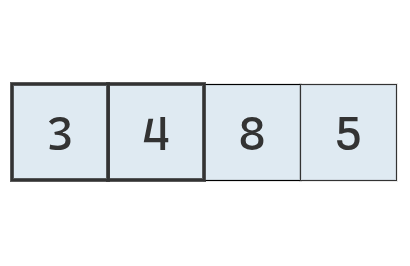
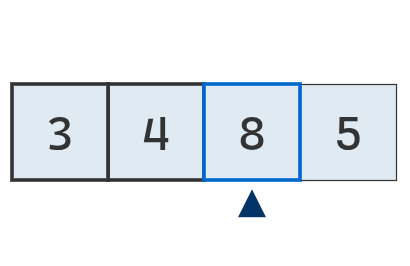
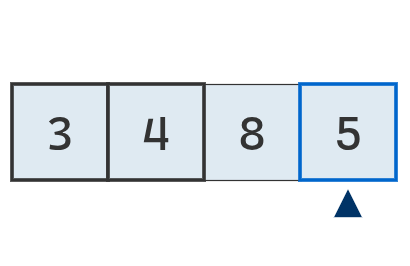
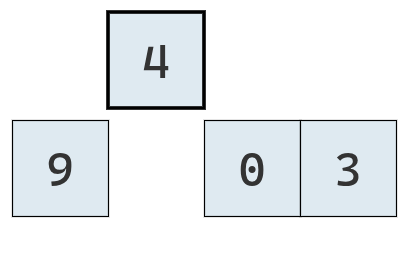
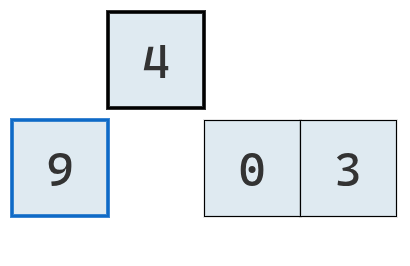
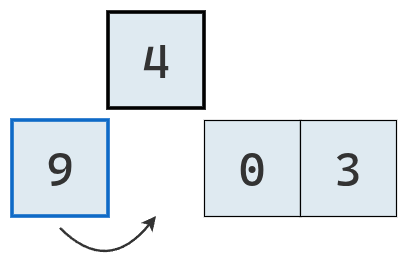
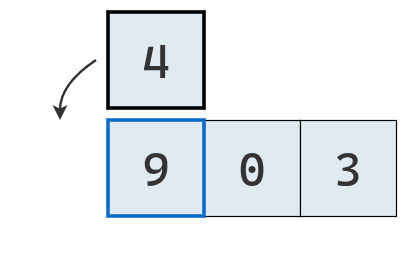
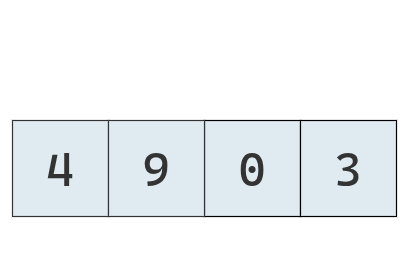
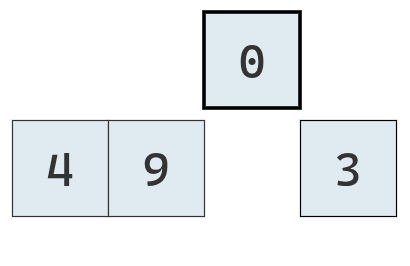
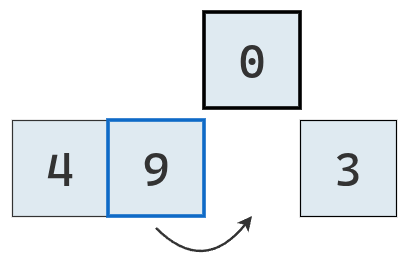
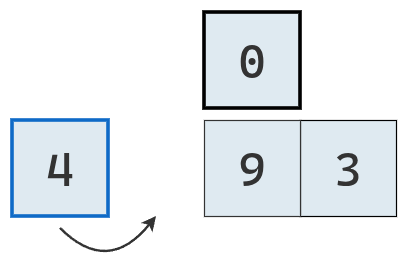
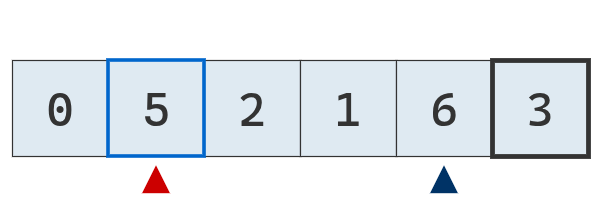
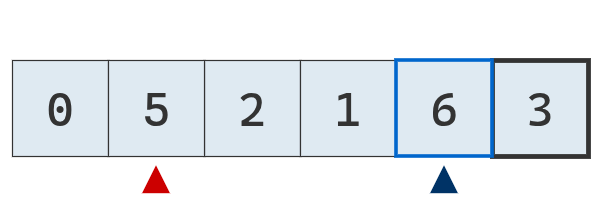
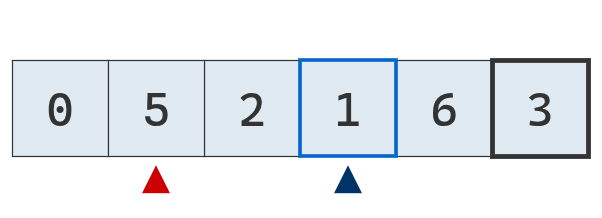
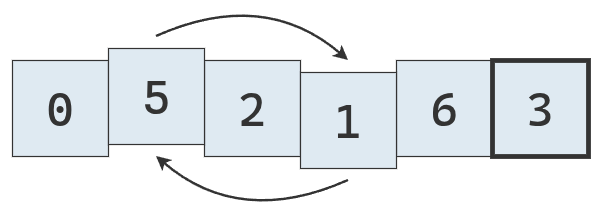
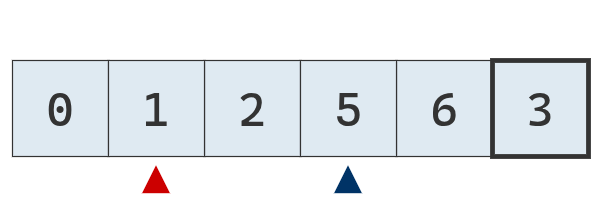
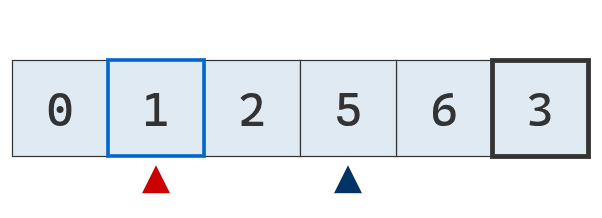
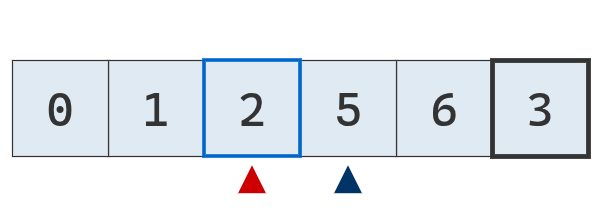
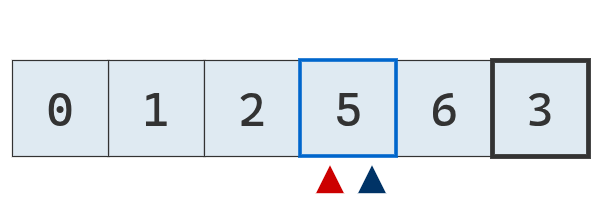
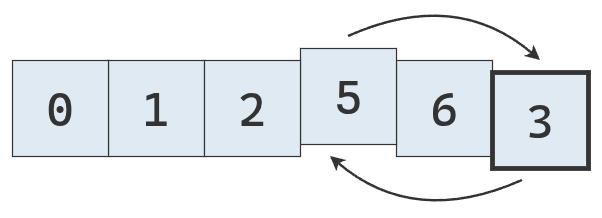
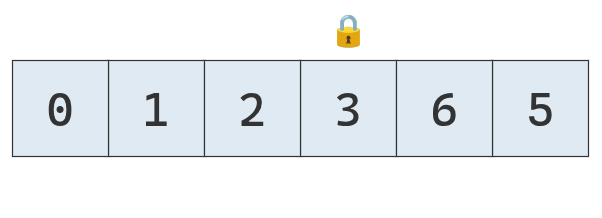
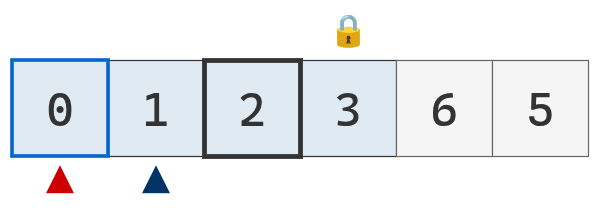
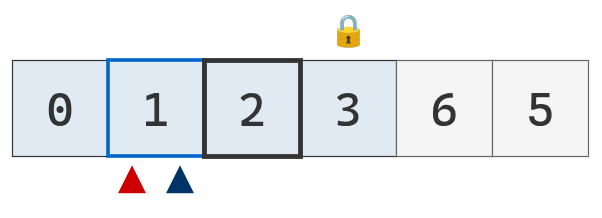
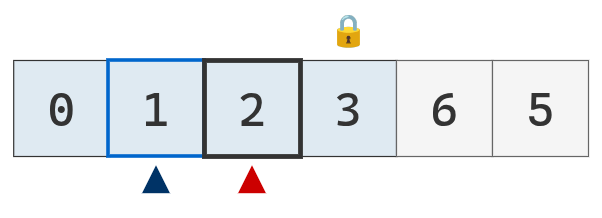
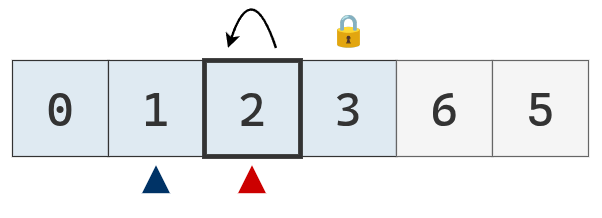
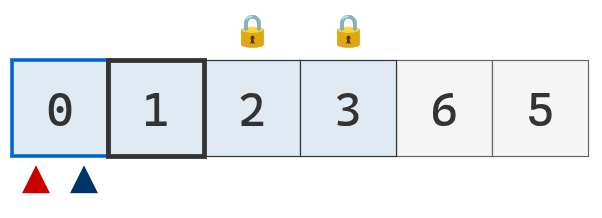
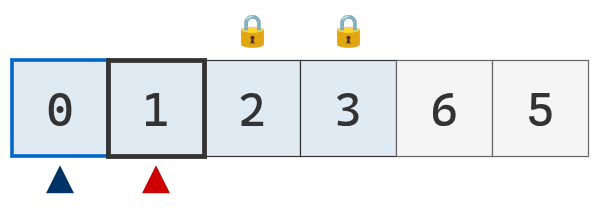
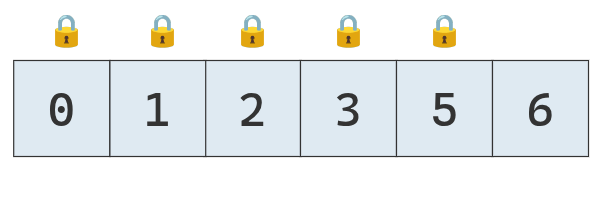
Veamos cómo funciona este procedimiento con la lista original [7, 2, 4, 5]:
El proceso que acabamos de observar es la base del algoritmo bubble sort. Más adelante volveremos sobre el origen del nombre.
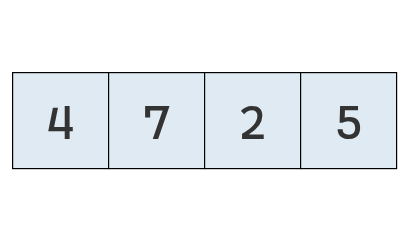
Ahora, debemos notar que obtuvimos una lista ordenada en tan pocos pasos de pura suerte. Para ver por qué, apliquemos el mismo conjunto de pasos sobre una lista con la misma cantidad de elementos, en un orden apenas diferente.
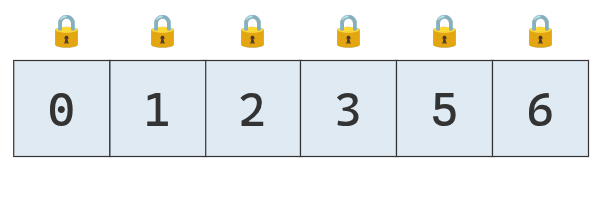
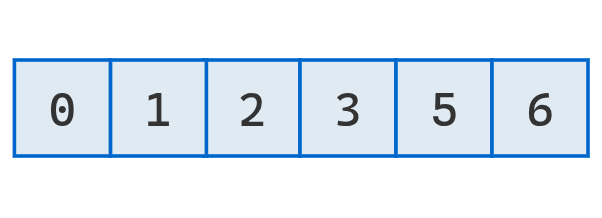
La primera vez que usamos el algoritmo, obtuvimos una lista ordenada. En la segunda, la lista quedó más ordenada que al inicio, pero aún no completamente.
Como mencionamos anteriormente, que en el primer caso se obtenga una lista ordenada al realizar una sola pasada fue simplemente una coincidencia.
El algoritmo bubble sort funciona realizando pasadas sucesivas sobre la lista, comparando pares de valores consecutivos, de principio a fin. En cada comparación, si un valor es mayor que el siguiente, se intercambian sus posiciones. Este proceso se repite hasta completar una pasada en la que no se realiza ningún intercambio; solo entonces puede concluirse que la lista está completamente ordenada.
Continuando el ejemplo, tenemos:
Implementación
def bubble_sort(arr):
arr = arr[:] # Hacer copia
n = len(arr)
1 intercambiado = True
2 while intercambiado:
3 intercambiado = False
4 for i in range(n - 1):
5 if arr[i] > arr[i + 1]:
# Se intercambian los valores
arr[i], arr[i + 1] = arr[i + 1], arr[i]
intercambiado = True
return arr- 1
-
Se usa una variable booleana
intercambiadopara indicar si en la pasada anterior se hizo un intercambio de elementos, y por lo tanto se debe realizar una pasada más. Inicialmente, este valor esTruepara que se ejecute el buclewhileal menos una vez. - 2
- Mientras se haya intercambiado en la pasada anterior.
- 3
-
El primer paso de cada pasada es igualar
intercambiadoaFalse. Solo cuando se haga un intercambio se lo convierte aTrue. - 4
- Se itera a través de todos los valores en la secuencia, excepto el último, ya que se comapran de a pares.
- 5
-
Si el valor de la posición
ies mayor que el de la posicióni + 1, se intercambian y se igualaintercambiadoaTrue.
bubble_sort([12, 9, 3, 6, 11, 5])
[3, 5, 6, 9, 11, 12]Esta versión repite pasadas completas hasta que no se produce ningún intercambio, lo que indica que la lista está ordenada.
En cada pasada, el algoritmo ubica el mayor valor fuera de orden en su posición correcta, al final de la lista. Este proceso hace que los valores más grandes “suban” gradualmente hacia la parte superior, como burbujas que ascienden en el agua, lo que da origen al nombre bubble sort.
En cada pasada, el mayor valor fuera de orden se coloca en su posición definitiva. Esto implica que en la primera pasada el valor máximo llega a la última posición, en la segunda el segundo mayor queda en la penúltima, y así sucesivamente.
Por lo tanto, en cada nueva pasada puede omitirse la última comparación, ya que los elementos finales ya están ordenados.
Hacer clic aquí.
Análisis de la eficiencia
El algoritmo bubble sort tiene dos tipos principales de pasos:
- Comparaciones: se comparan números de a pares para determinar cuál es mayor.
- Intercambios: se intercambian números para ordenarlos.
Supongamos que tenemos una lista de 5 números y usamos una implementación eficiente, que omite las comparaciones innecesarias al final del arreglo.
En la primera pasada se realizan 4 comparaciones, en la segunda 3, en la tercera 2 y en la última 1. En total, se efectúan 4 + 3 + 2 + 1 = 10 comparaciones.
De manera general, si el arreglo tiene \(N\) elementos, el número máximo de comparaciones es:
\[ (N - 1) + (N - 2) + \cdots + 2 + 1 = \frac{N(N - 1)}{2} = \frac{N^2}{2} - \frac{N}{2} \]
Además, en el peor de los casos (cuando la lista está ordenada en forma descendente), será necesario realizar tantos intercambios como comparaciones, ya que en cada comparación habrá un valor mayor a su derecha. El total de comparaciones e intercambios posibles es entonces:
\[ 2 \left[\frac{N^2}{2} - \frac{N}{2}\right] = N^2 - N \]
Así, se concluye que la complejidad temporal de bubble sort \(O(N^2)\). Aunque la cantidad de pasos no solo dependa \(N^2\), sino también de \(N\), la notación Big O se centra en el orden del término dominante y, en este caso, se dice que buble sort es de complejidad cuadrática.
La siguiente tabla muestra lo rápido que crece la cantidad máxima de pasos conforme se incrementa la cantidad de elementos a ordenar:
| \(N\) | Cantidad máxima de pasos |
|---|---|
| 5 | 20 |
| 10 | 90 |
| 20 | 380 |
| 30 | 870 |
| 50 | 2450 |
| 100 | 9900 |
Selection sort
Otro algoritmo sencillo para ordenar una secuencia es selection sort. Al igual que bubble sort, realiza múltiples pasadas a través de la lista.
Su particularidad es que en cada pasada selecciona el menor valor de la parte desordenada y lo coloca en la posición que le corresponde.
Luego, continúa con el resto de la lista, repitiendo el proceso hasta que todos los elementos quedan ordenados.
Implementación
def selection_sort(arr):
arr = arr[:]
1 for i in range(len(arr) - 1):
2 indice_menor_numero = i
3 for j in range(i + 1, len(arr)):
if arr[j] < arr[indice_menor_numero]:
indice_menor_numero = j
4 if indice_menor_numero != i:
arr[i], arr[indice_menor_numero] = arr[indice_menor_numero], arr[i]
return arr- 1
-
El puntero
iitera desde el primer hasta el penúltimo elemento. Este es el que realiza las pasadas. - 2
-
En cada pasada, se toma al primer valor como el mínimo, por eso
indice_menor_numerose iguala ai. - 3
-
Otro puntero,
j, recorre la lista a partir dei, hasta el final. Si el valor en la posiciónjes mejor que en el mínimo actual, se toma ajcomo el índice con el mínimo. - 4
- Si el mínimo no está al principio de la sublista que se recorre, se intercambian las posiciones de los elementos para que el mínimo esté al principio.
selection_sort([95, 50, 20, 13, 17, 100])
# [13, 17, 20, 50, 95, 100]Hacer clic aquí.
Análisis de eficiencia
Al igual que bubble sort, el algoritmo selection sort también utiliza dos tipos de operaciones: comparaciones e intercambios. En cada pasada, se compara cada valor de la parte desordenada con el mínimo actual, y al finalizar se coloca dicho mínimo en su posición correcta (intercambiándolo con el valor que estaba allí).
La cantidad de comparaciones que realiza es idéntica a la del algoritmo bubble sort. Para un arreglo de longitud \(N\), se efectúan \(\frac{N^2}{2} - \frac{N}{2}\) comparaciones.
Por otro lado, y a diferencia del algoritmo bubble sort, se realiza a lo sumo un intercambio por pasada, por lo que en total pueden realizar hasta \(N - 1\) intercambios y la cantidad máxima de pasos del algoritmo insertion sort es:
\[ \frac{N^2}{2} - \frac{N}{2} + (N - 1), \]
lo que indica que la complejidad temporal de selection sort también es cuadrática.
La siguiente tabla muestra una comparación lado a lado entre los dos algoritmos estudiados:
| N | Pasos máximos en bubble sort | Pasos máximos en selection sort |
|---|---|---|
| 5 | 20 | 14 (10 comparaciones + 4 intercambios) |
| 10 | 90 | 54 (45 comparaciones + 9 intercambios) |
| 20 | 380 | 209 (190 comparaciones + 19 intercambios) |
| 30 | 870 | 464 (435 comparaciones + 29 intercambios) |
| 50 | 2450 | 1274 (1225 comparaciones + 49 intercambios) |
| 100 | 9900 | 5049 (4950 comparaciones + 99 intercambios) |
De esta comparación se observa que selection sort requiere aproximadamente la mitad de los pasos que bubble sort, lo que indica que, en promedio, resulta alrededor de dos veces más rápido.
A pesar de que el algoritmo selection sort realiza aproximadamente la mitad de pasos que bubble sort, ambos se consideran algoritmos de complejidad cuadrática.
Al analizar la eficiencia mediante la notación Big O, solo importa cómo crece el número de pasos con el tamaño del problema, no la constante que los multiplica.
Si un algoritmo realiza \(N^2\) pasos y otro realiza \(N^2 / 2\), ambos crecen de manera proporcional a \(N^2\) cuando \(N\) aumenta.
Por lo tanto, tanto bubble sort como selection sort se describen como algoritmos de orden \(O(N^2)\).
Insertion sort
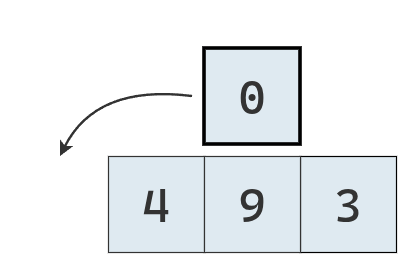
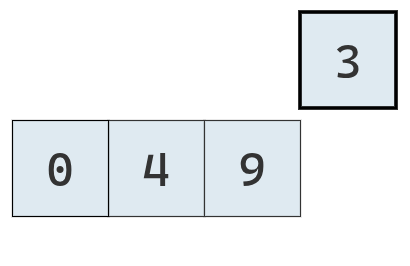
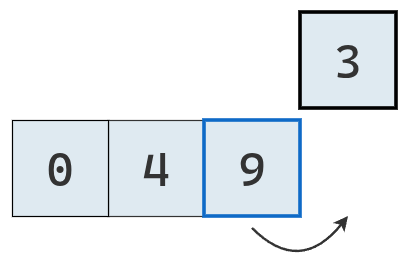
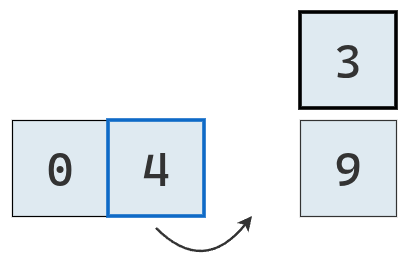
En esta sección estudiaremos otro algoritmo, llamado insertion sort. Es un método de ordenamiento simple que inserta los elementos de la lista en una sublista ordenada que ocupa las primeras posiciones.
Inicialmente, esta sublista ordenada contiene un solo elemento, el primero de la lista. A medida que se procesan los siguientes elementos, se van insertando en la posición correcta dentro de la sublista, manteniendo el orden. De esta forma, la parte ordenada va creciendo progresivamente hasta abarcar todos los elementos, momento en el cual la lista queda completamente ordenada.
Implementación
def insertion_sort(arr):
arr = arr[:]
1 for i in range(1, len(arr)):
valor_i = arr[i]
2 puntero = i - 1
3 while puntero >= 0 and arr[puntero] > valor_i:
arr[puntero + 1] = arr[puntero]
puntero -= 1
4 arr[puntero + 1] = valor_i
return arr- 1
-
La variable
ies la posición original del elemento a insertar en la lista ordenada. Se empieza del segundo elemento. Su valor lo representavalor_i. - 2
-
Un
punterorecorre de derecha a izquierda los elementos a la izquierda de la posicióni. - 3
-
Si el puntero no llegó al final y el valor en su posición es mayor al valor a insertar en la sublista ordenada (
valor_i), se mueve el valor en la posición del puntero a la derecha y se decrementa el puntero en 1 unidad. - 4
-
Una vez que termina el proceso de traslación de valores, se inserta el
valor_ien la posición que le corresponde, que es a la derecha delpuntero.
insertion_sort([9, 7, 5, 999, 1, 10, 25])
# [1, 5, 7, 9, 10, 25, 999]Hacer clic aquí.
Análisis de eficiencia
El algoritmo insertion sort realiza cuatro tipos de operaciones: extracciones, comparaciones, desplazamientos e inserciones.
Las comparaciones ocurren cada vez que se compara el valor_actual con los elementos que tiene a su izquierda. En el peor de los casos, cuando la lista está ordenada en sentido descendente, todos los valores a la izquierda son mayores que valor_actual, lo que obliga con compararlo con todos ellos antes de volver a insertarlo.
En la primera pasada se realiza 1 comparación, en la segunda 2, y así sucesivamente, hasta la última pasada donde se realizan \(N - 1\) comparaciones. Por lo tanto, el número máximo de comparaciones es:
\[ 1 + 2 + 3 + \dots + (N - 1) = \frac{N^2}{2} - \frac{N}{2} \]
Los desplazamientos ocurren cada vez que un valor se mueve a la derecha para dejar lugar al valor_actual. En el peor de los casos, el número de desplazamientos es igual al número de comparaciones. Sumando ambos tipos de operaciones, el número total de pasos es \(N^2 - N\).
Por su parte, las extracciones e inserciones se realizan una vez por pasada, es decir, \(N - 1\) veces cada una. Estas operaciones tienen un peso menor frente al crecimiento cuadrático de las comparaciones y desplazamientos.
El número total de pasos es entonces:
\[ N^2 - N + 2N - 2 = N^2 + N - 2 \]
En términos de notación Big O, que no solo descarta términos constantes, sino que también se concentra en el término de mayor orden, concluimos que el algoritmo es de orden \(O(N^2)\).
Analizando el “caso promedio”
Hasta ahora, el análisis se centró siempre en el peor escenario, pero el desempeño de insertion sort depende en gran medida del orden inicial de los datos.
En el peor de los casos, cuando el arreglo está ordenado de manera decreciente, insertion sort tiene una complejidad de \(O(N^2)\). En esta situación, su desempeño resulta inferior al de selection sort, que requiere menos operaciones (alrededor de \(O(N^2/2)\)).
Si los datos ya están ordenados, insertion sort solo realiza una comparación por pasada y ningún desplazamiento, sumando en total \(N - 1\) comparaciones. Selection sort, por su parte, efectuaría igualmente unas \(\frac{N^2}{2} - \frac{N}{2}\) comparaciones.
Cuando los datos no siguen ningún orden en particular, insertion sort tiene pasadas en las que compara y traslada todos, algunos o ninguno de los valores. Si en el peor caso se comparan y trasladan todos los elementos, y en el mejor no se traslada ninguno, podemos estimar que, en un caso promedio, se comparará y trasladará aproximadamente la mitad de los elementos. Por eso se representa con una complejidad de \(O(N^2/2)\).
En resumen, mientras selection sort mantiene una complejidad constante de \(O(N^2/2)\) sin importar el orden inicial de los datos, _insertion sort? varía entre \(O(N)\) en el mejor de los casos, \(O(N^2/2)\) en el promedio y \(O(N^2)\) en el peor.
La elección de cuál usar depende, en definitiva, de las características de los datos a ordenar. Por su eficiencia en listas casi ordenadas, insertion sort suele utilizarse dentro de algoritmos más complejos como parte de etapas finales de ordenamiento.
Divide y vencerás
Los tres algoritmos que estudiamos hasta ahora nos sirvieron para comprender los fundamentos de los algoritmos de ordenamiento, practicar el análisis de la complejidad temporal y reforzar la idea de que no existe una única forma de ordenar.
Sin embargo, la complejidad temporal de todos ellos está lejos de ser ideal. Cuando un algoritmo tiene complejidad cuadrática, incluso un pequeño incremento en el tamaño \(N\) de la secuencia puede hacer que el número de pasos necesarios crezca de manera considerable.
Por estos motivos, y dado que existen alternativas más eficientes, ningún lenguaje de programación maduro utiliza alguno de estos algoritmos como método de ordenamiento por defecto.
En la práctica, se prefieren algoritmos más elaborados que logran una mejora sustancial en el desempeño computacional. Dos ejemplos clásicos de estos son merge sort y quick sort.
Ambos se basan en un mismo paradigma de diseño algorítmico conocido como divide y vencerás (del inglés, divide and conquer). Este enfoque consiste en resolver un problema grande de forma recursiva, dividiéndolo en subproblemas más pequeños del mismo tipo.
La idea clave es que ordenar secuencias pequeñas resulta mucho más rápido que ordenar una grande, y que ordenar una secuencia parcialmente ordenada es más eficiente que hacerlo sobre una totalmente desordenada.
De manera general, el método divide y vencerás se desarrolla en tres etapas, que en el contexto del ordenamiento pueden describirse así:
- Dividir: Si la secuencia \(S\) es lo suficientemente pequeña (por ejemplo, contiene uno o dos elementos), se la ordena directamente y se devuelve un resultado. En caso contrario, se divide \(S\) en dos o más subsecuencias disjuntas.
- Conquistar: se aplica el mismo procedimiento recursivamente sobre cada subsecuencia hasta que todas estén ordenadas.
- Combinar: se toman las subsecuencias ordenadas y se las une para formar una única secuencia ordenada, que constituye la solución final al problema original.
A continuación veremos cómo estos pasos se materializan en un caso particular: merge sort.
Merge sort
Merge sort es un algoritmo recursivo que divide continuamente una lista por la mitad. Si la lista está vacía o contiene un solo elemento, se considera ordenada por definición (caso base). En cambio, si tiene más de un elemento, se divide y se aplica recursivamente merge sort a cada mitad (caso recursivo).
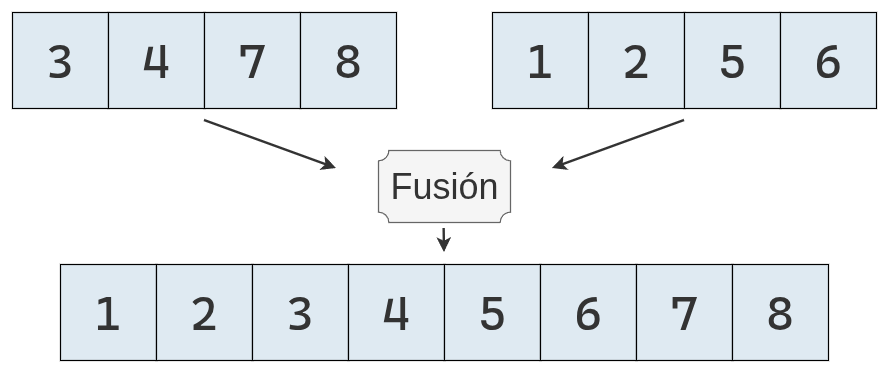
Una vez que ambas mitades están ordenadas, se realiza la operación fundamental del algoritmo, llamada fusión (del inglés, merge). La fusión consiste en combinar dos listas ordenadas más pequeñas en una única lista nueva y ordenada.
El procedimiento general del algoritmo puede resumirse así:
- Dividir: si la secuencia \(S\) tiene 0 o 1 elementos, se devuelve directamente porque ya está ordenada. En otro caso, se divide en dos subsecuencias: la primera mitad en \(S_1\) y la segunda en \(S_2\).
- Ordenar (Conquistar): aplicar recursivamente merge sort sobre \(S_1\) y \(S_2\).
- Fusionar: combinar las secuencias ordenadas \(S_1\) y \(S_2\) para obtener una nueva secuencia ordenada que contiene todos los elementos de \(S\).
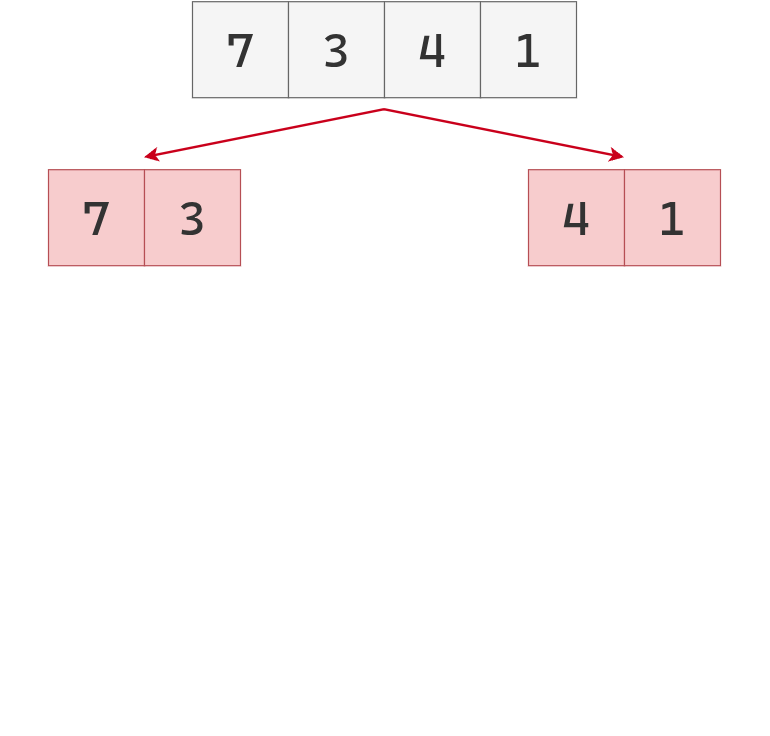
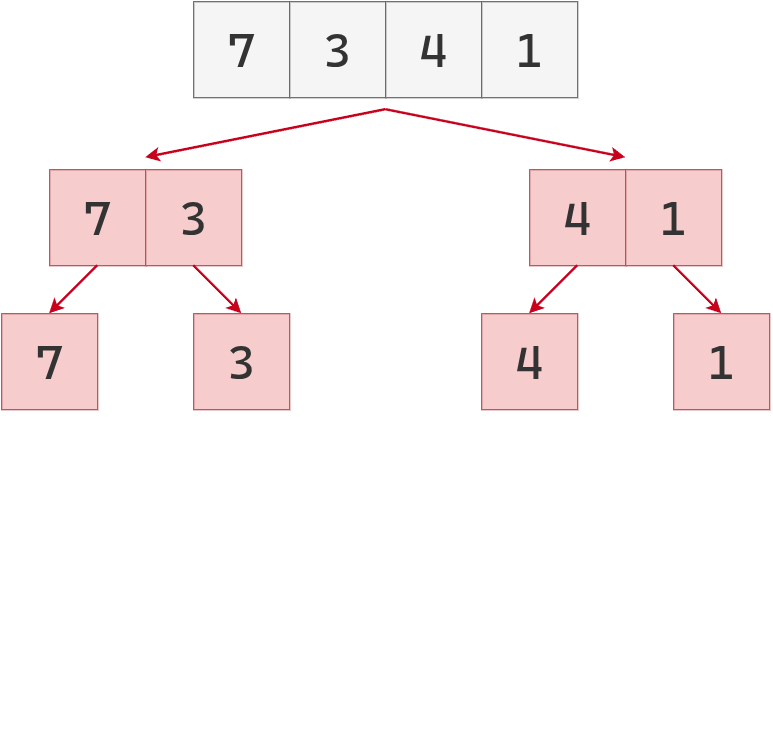
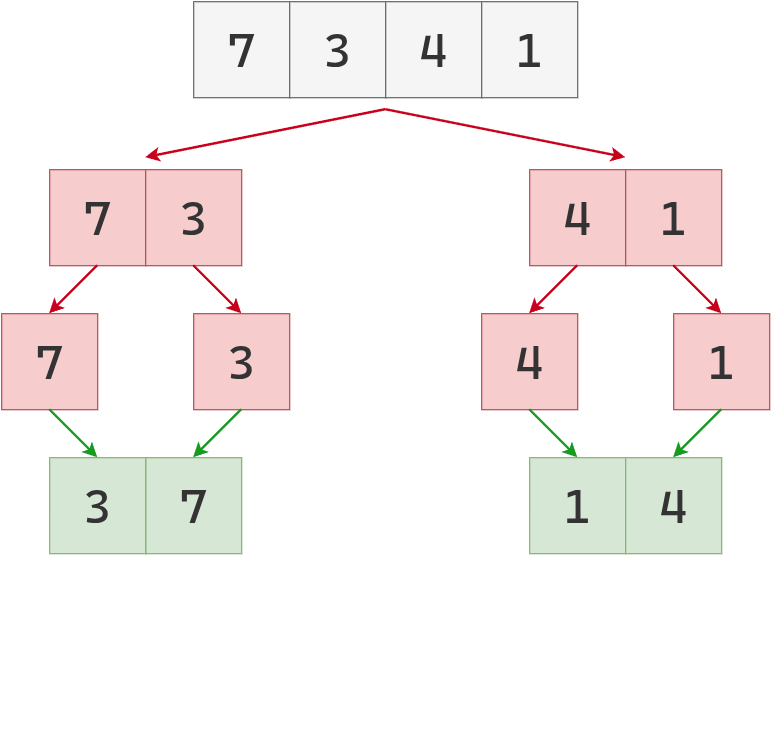
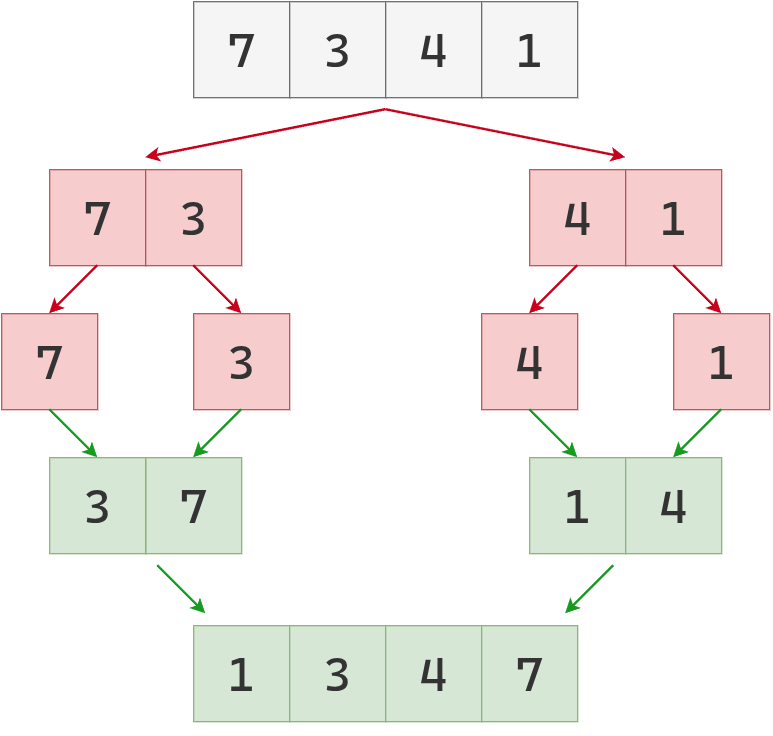
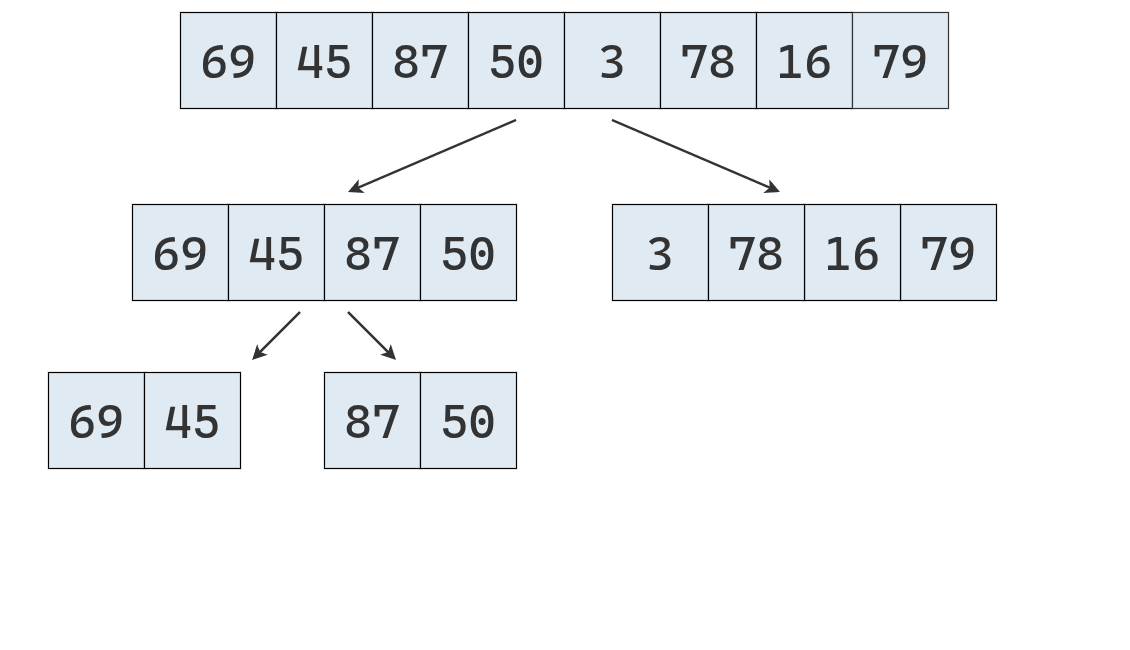
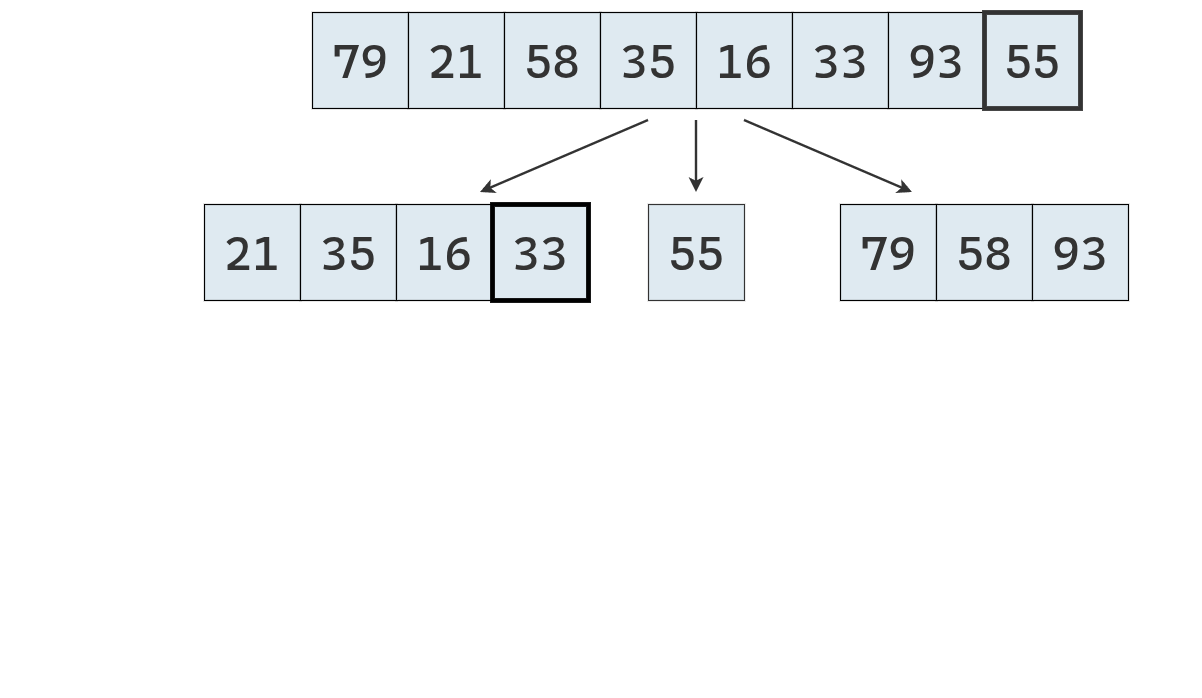
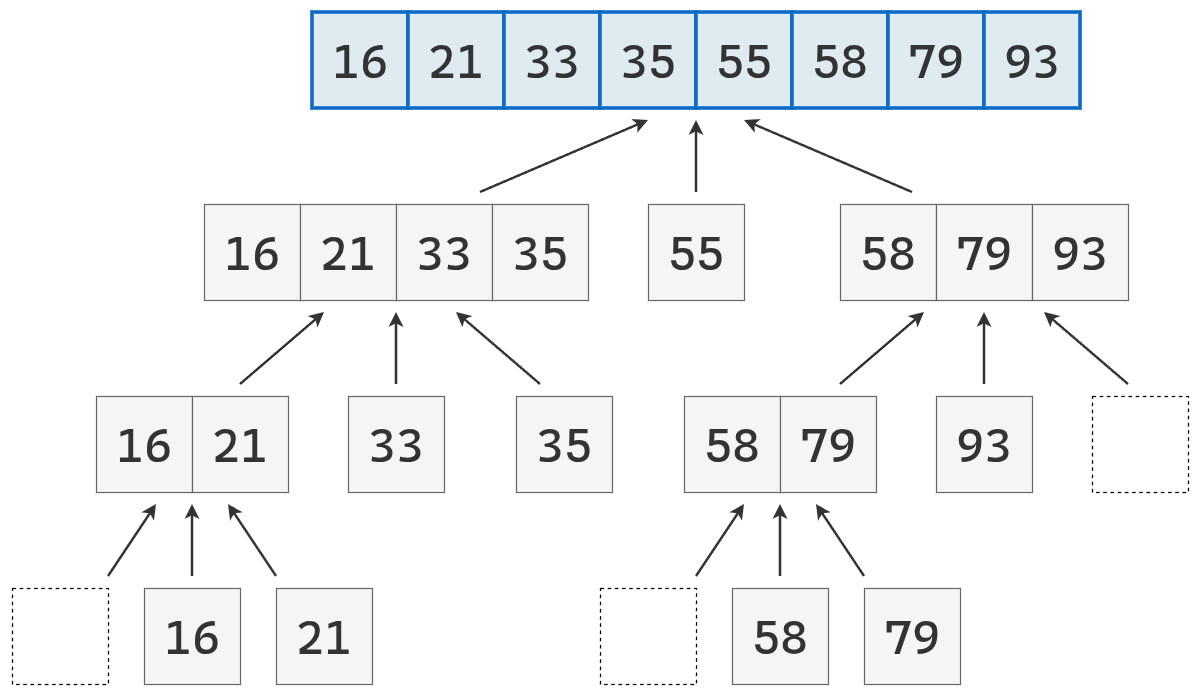
Visualmente:
Esta representación esquemática ayuda a visualizar la aplicación del principio divide y vencerás en un algoritmo de ordenamiento como merge sort.
Sin embargo, esta representación no refleja fielmente el funcionamiento del algoritmo, considerando su naturaleza recursiva.
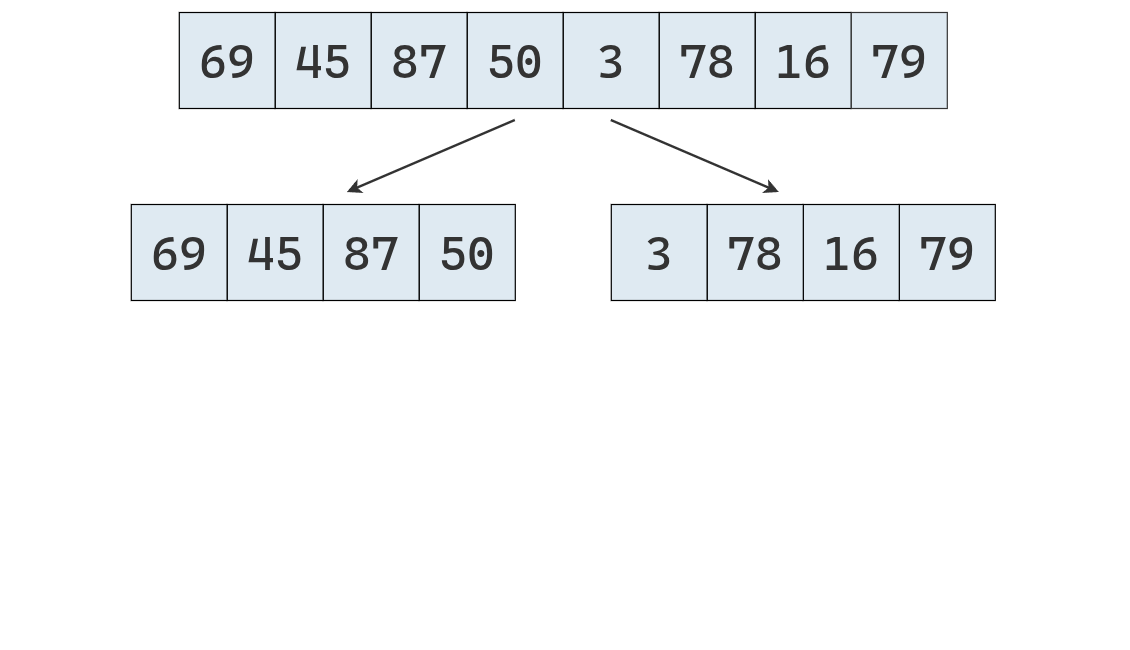
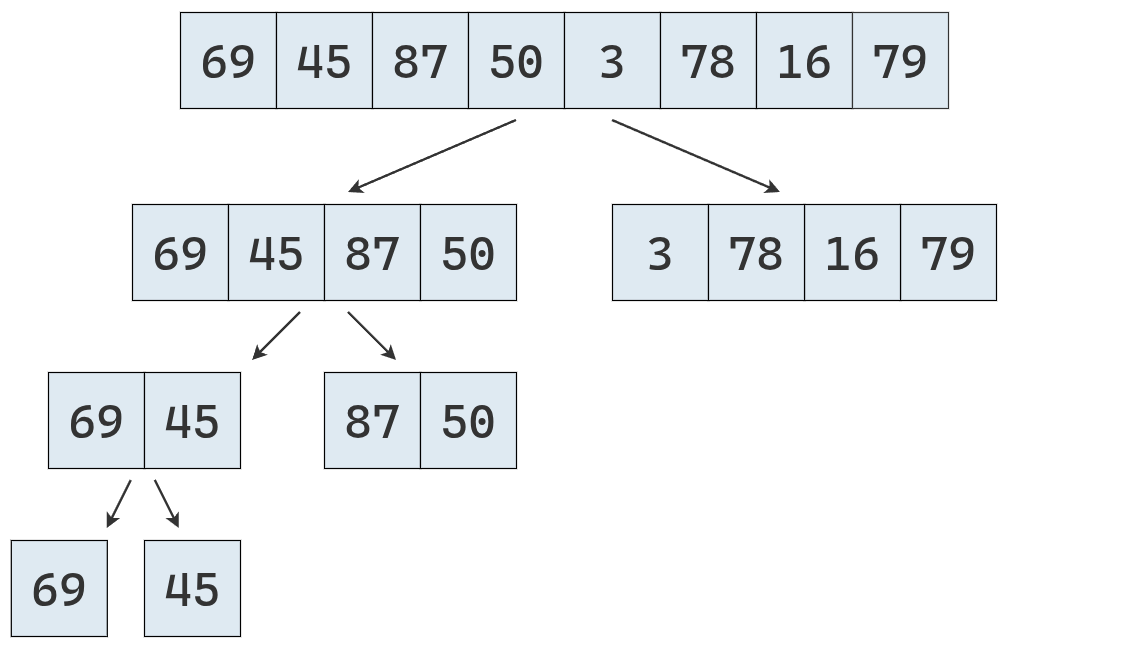
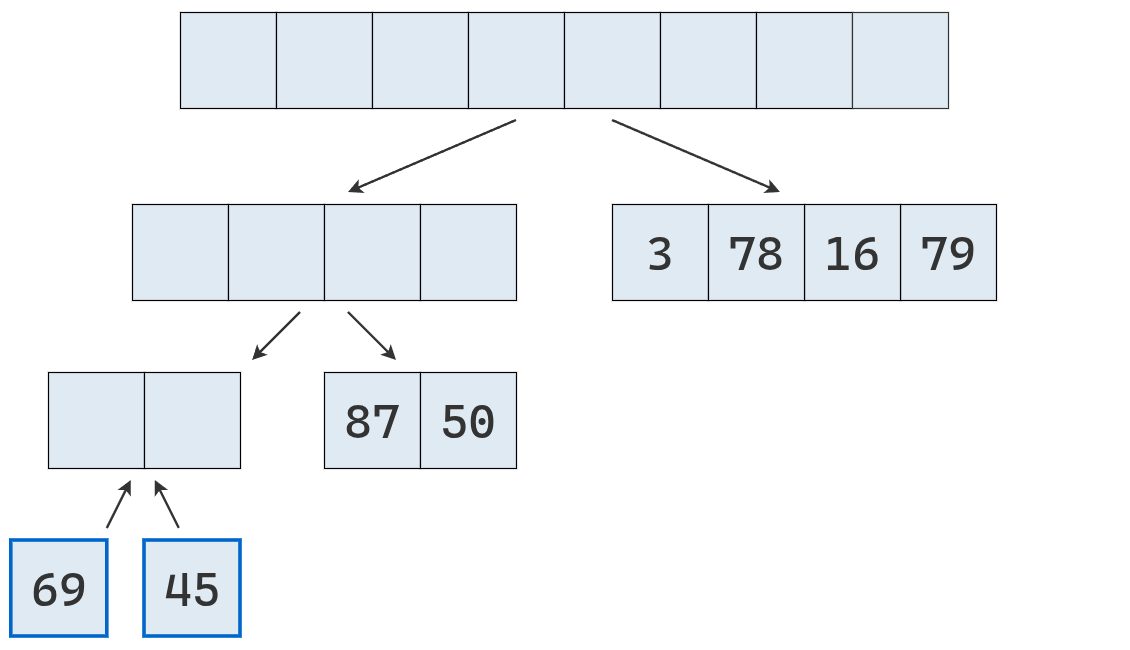
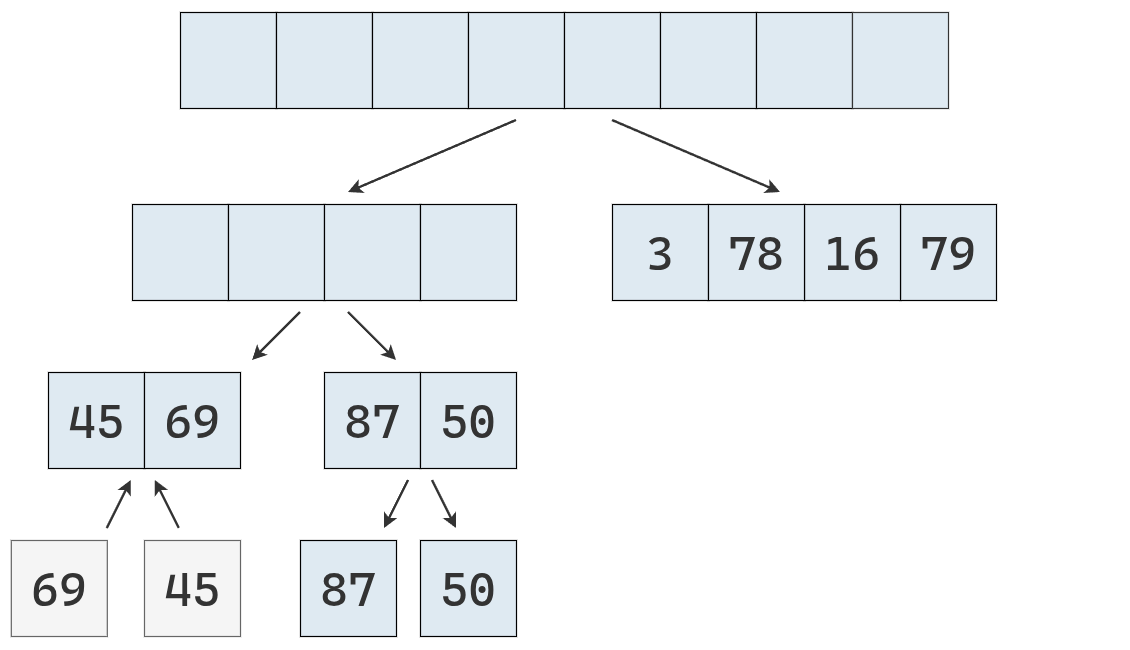
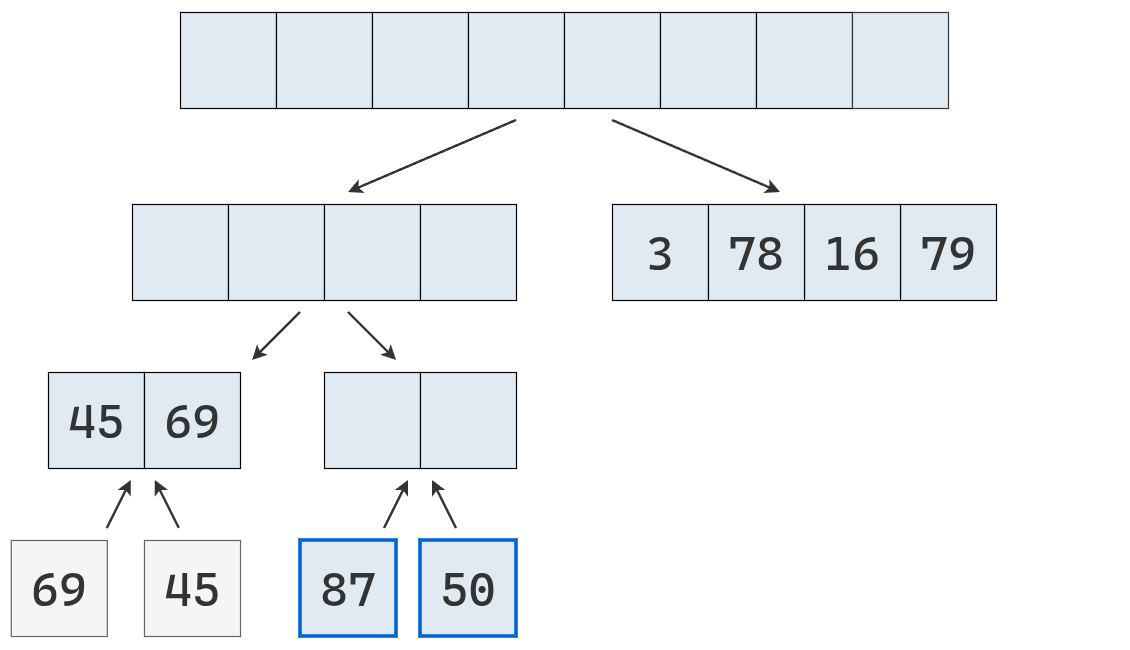
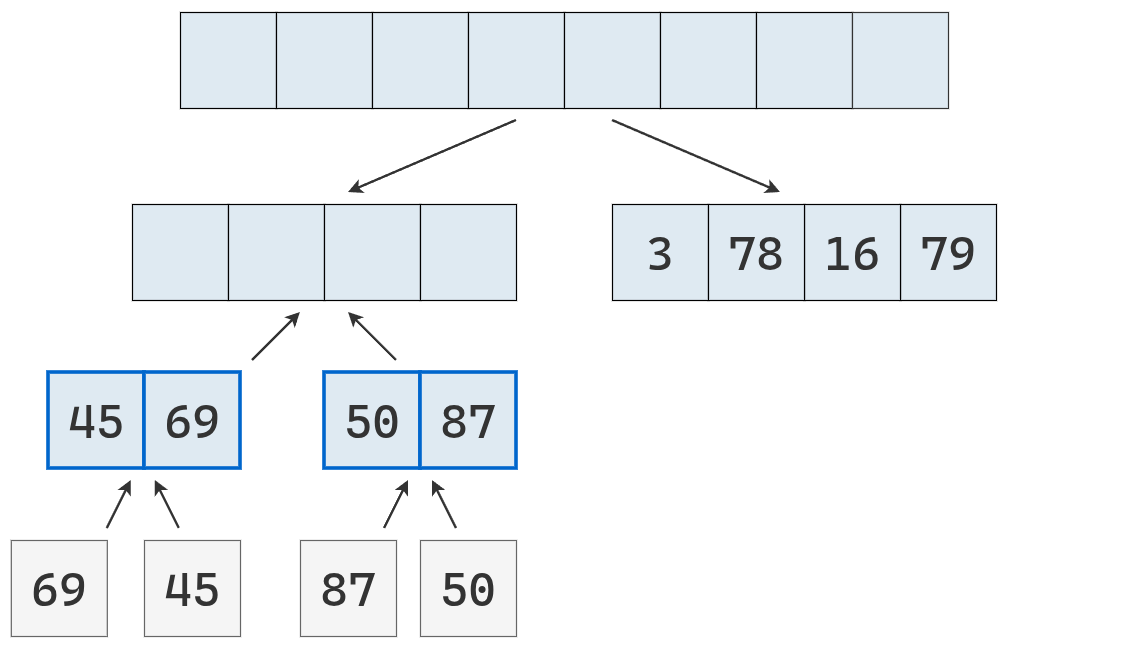
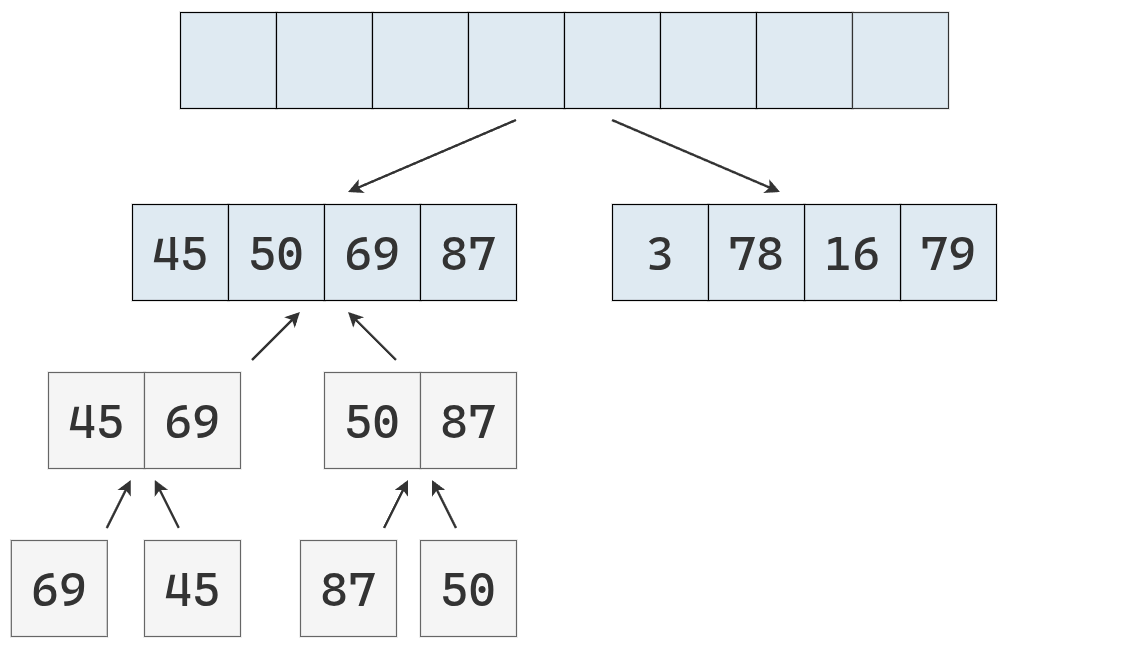
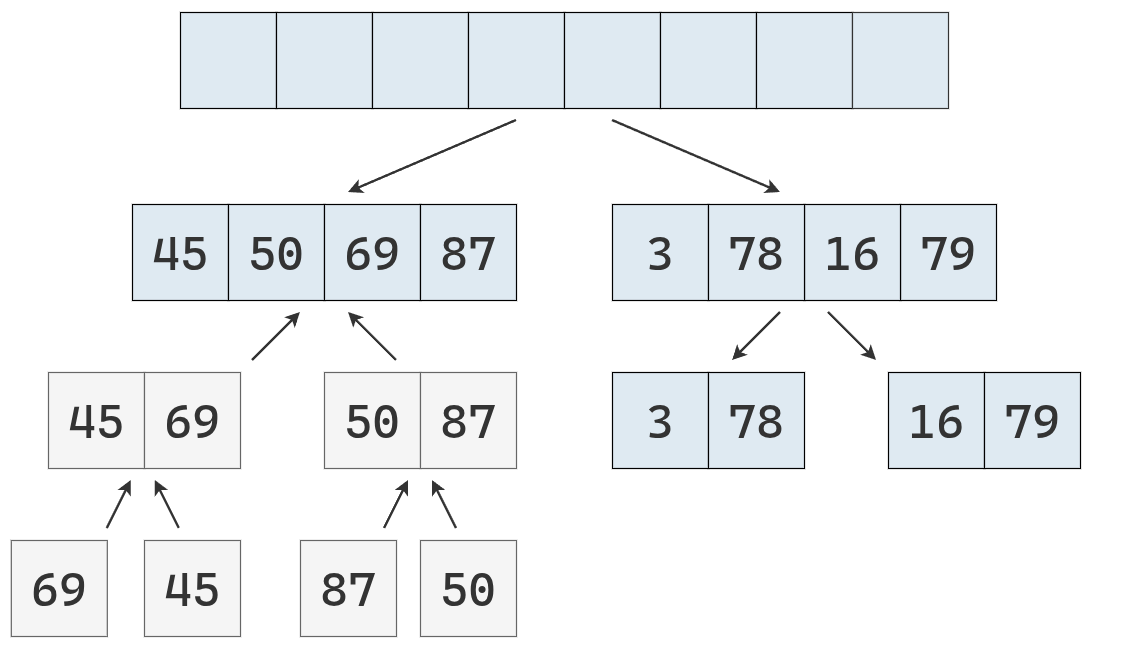
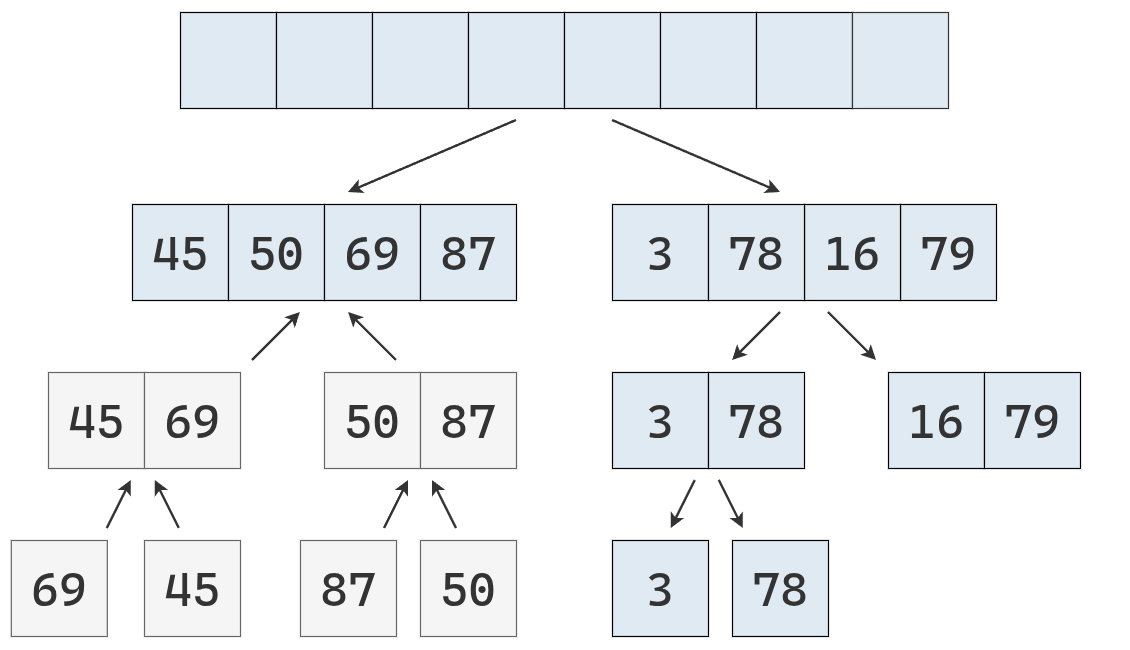
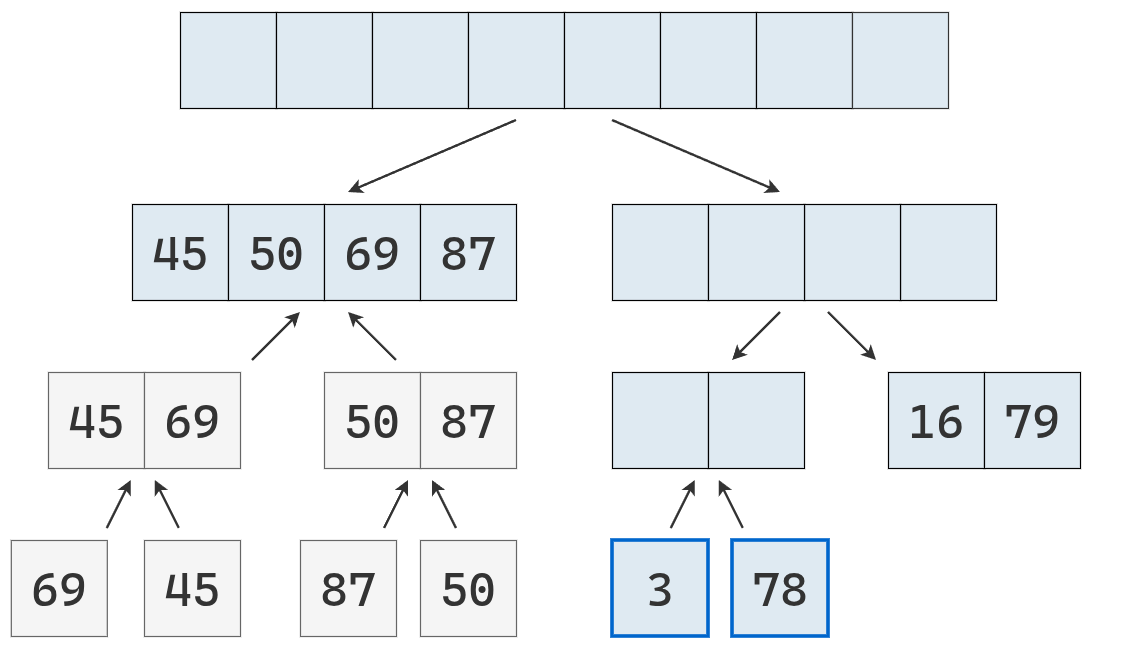
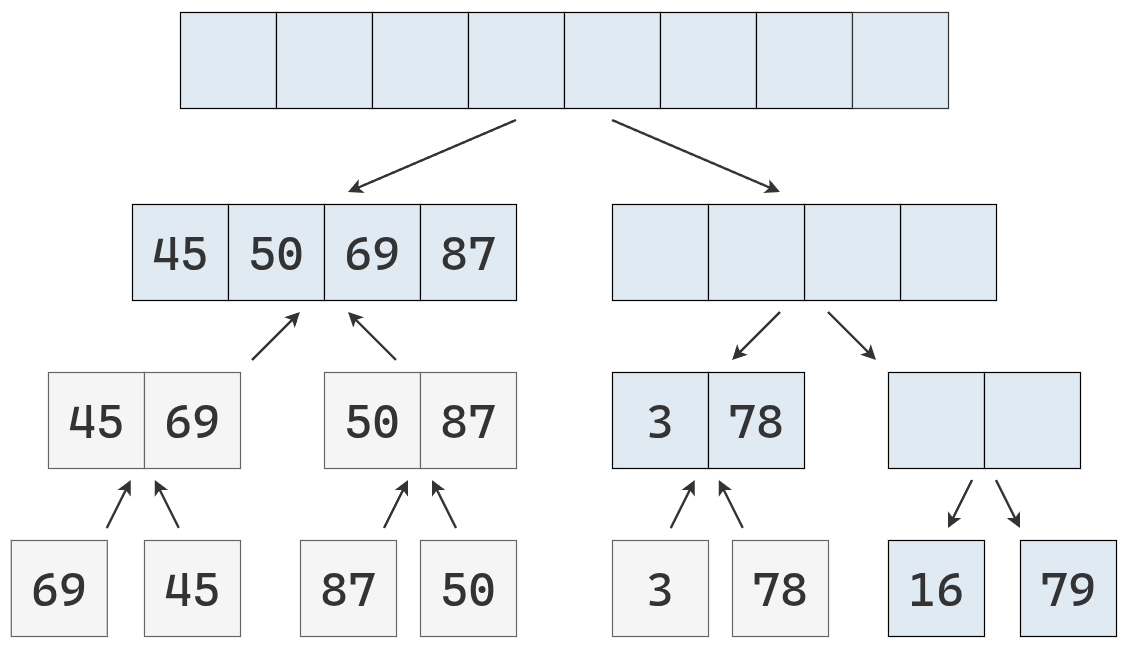
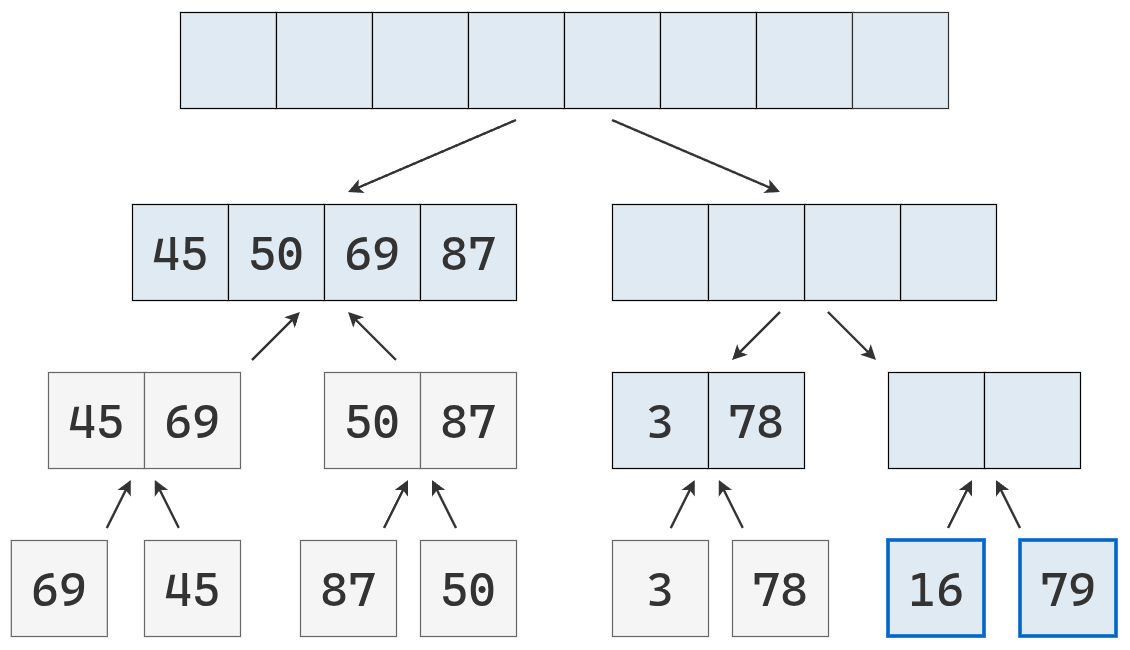
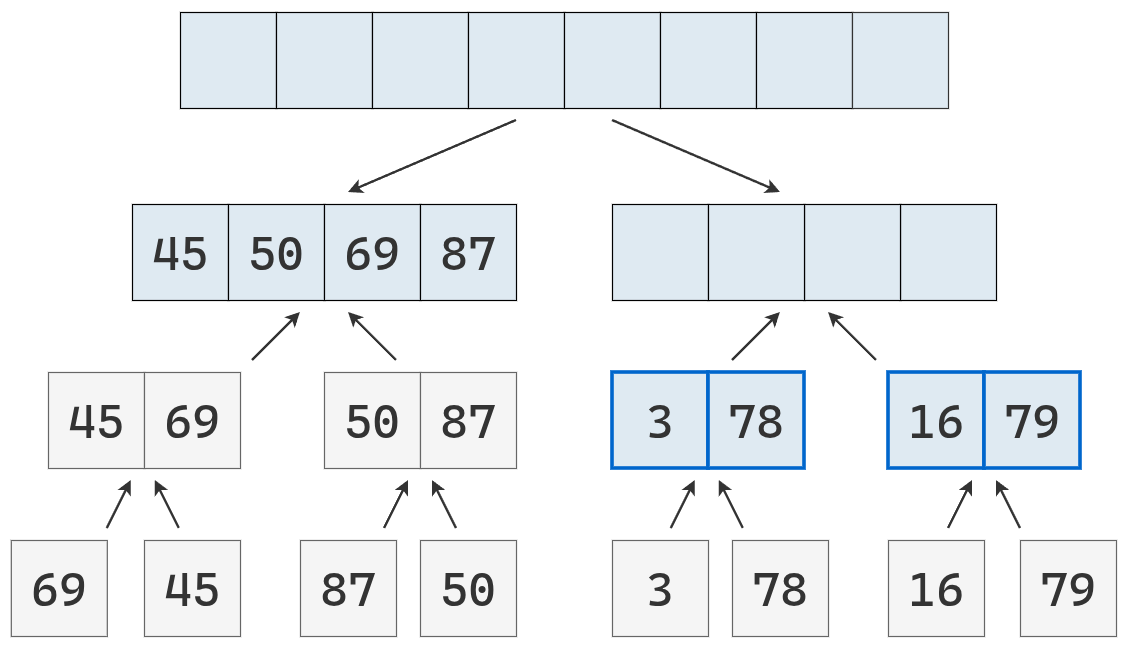
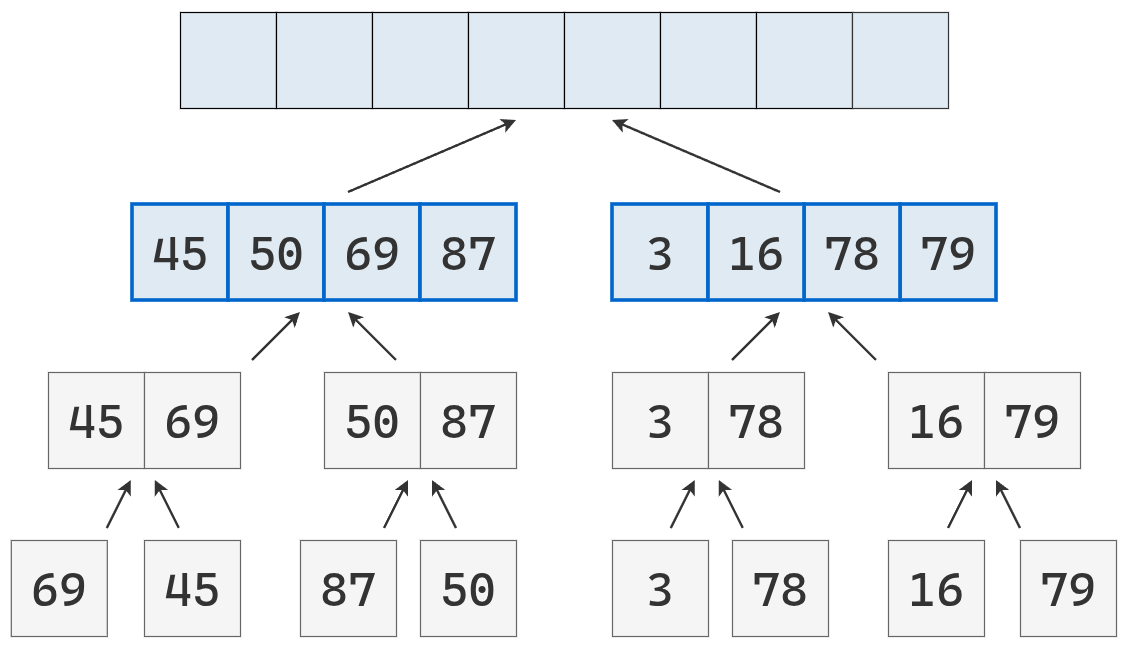
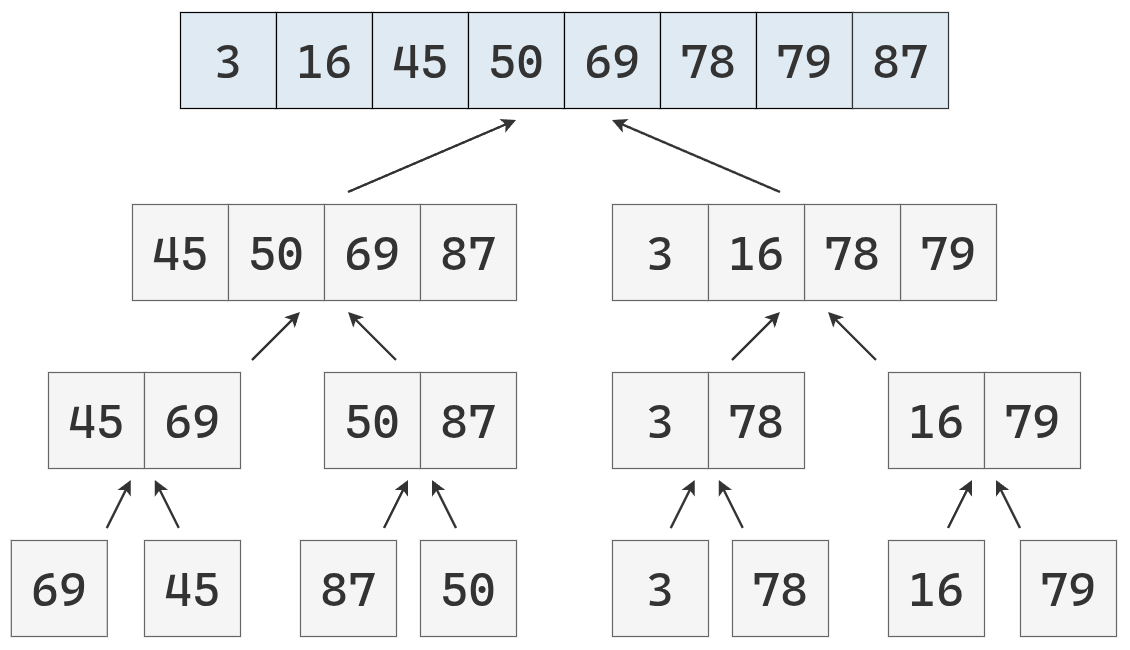
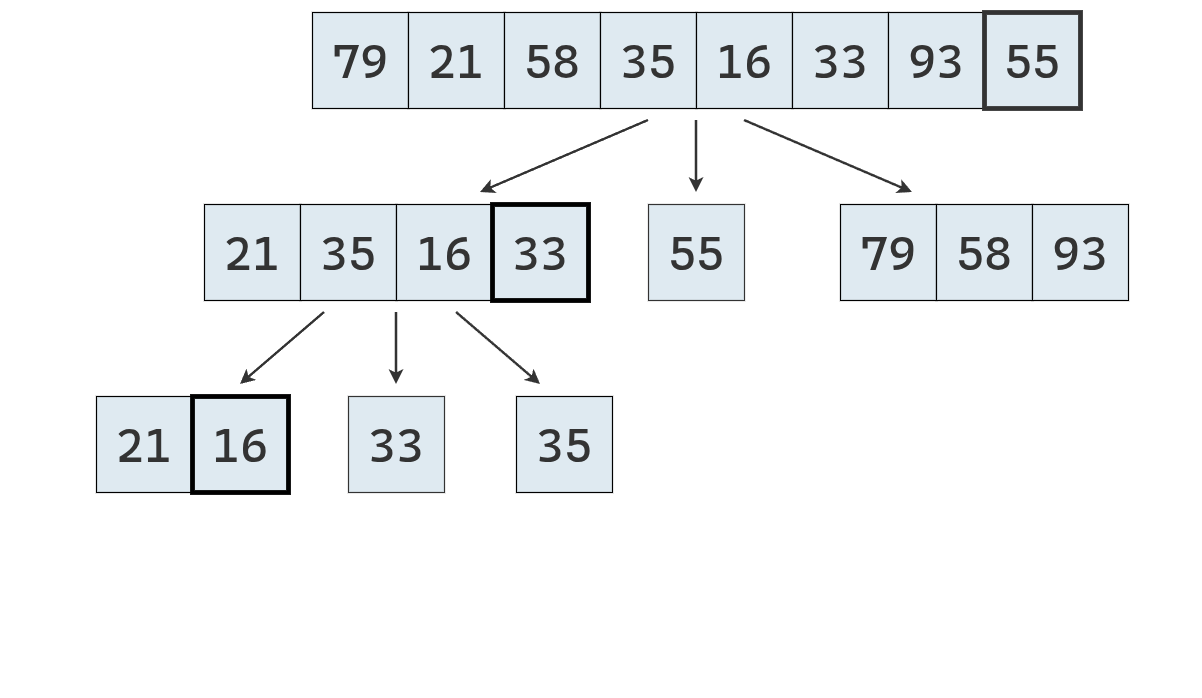
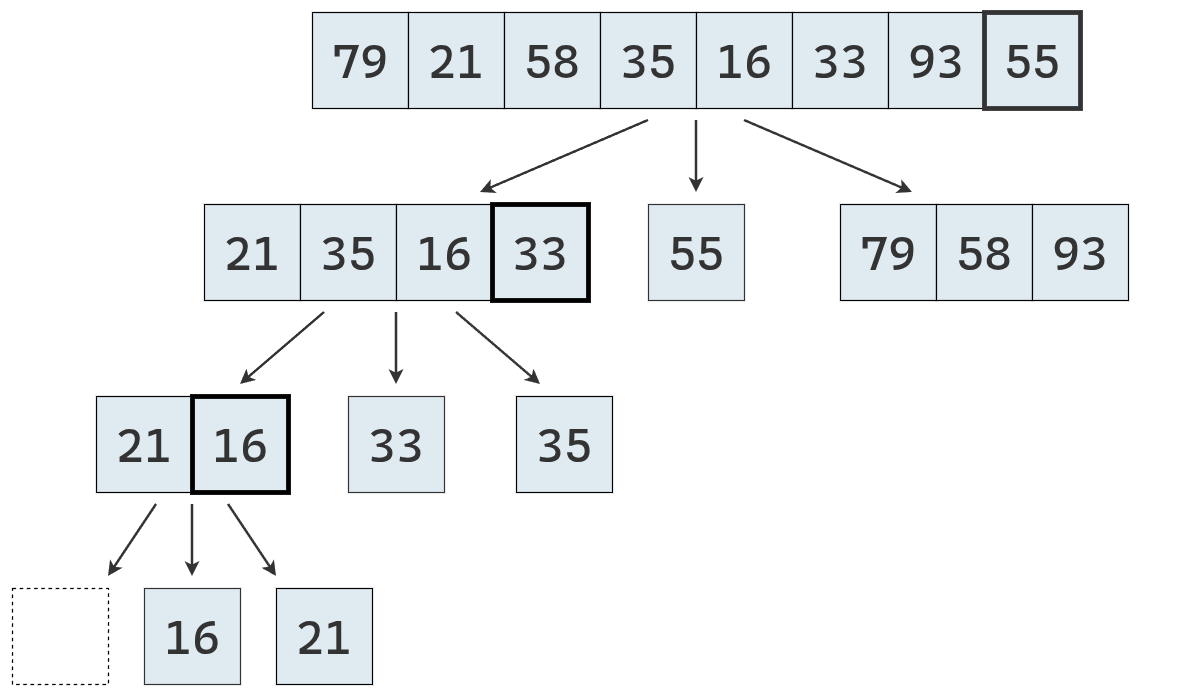
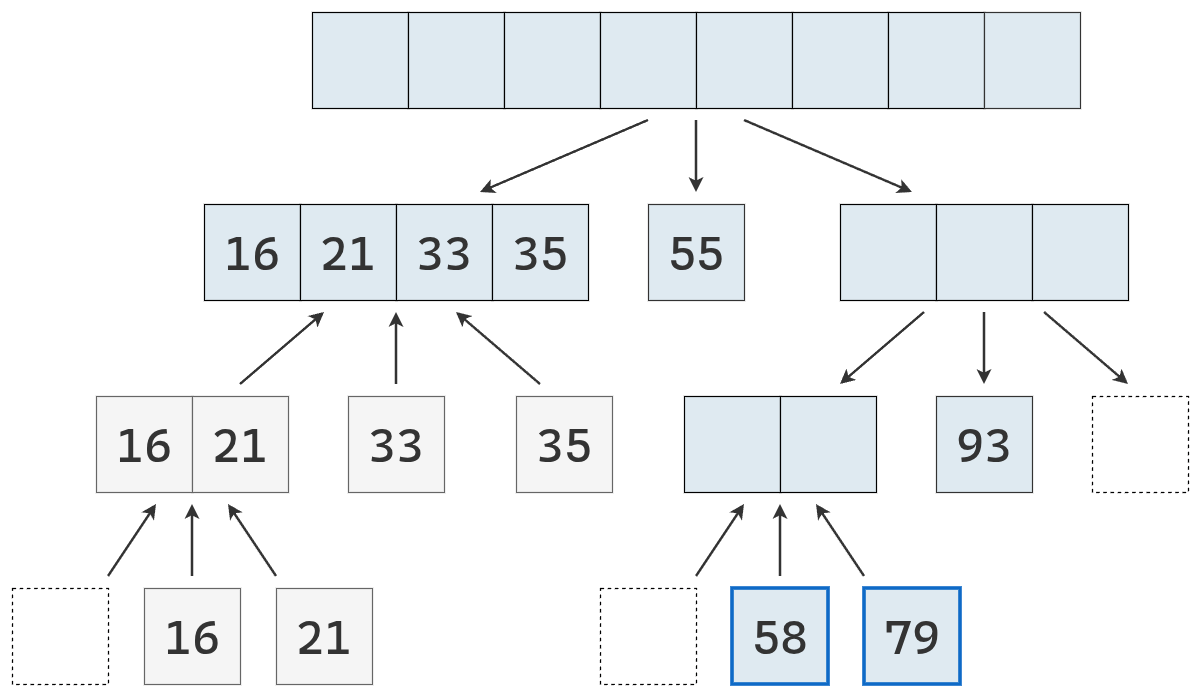
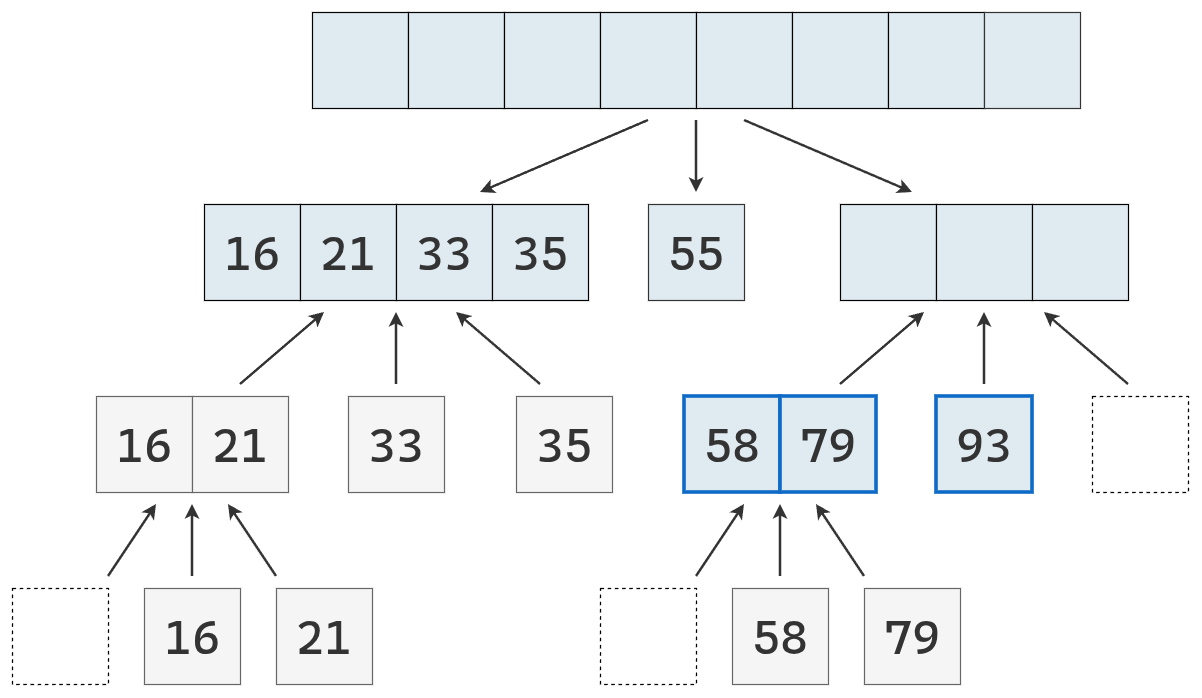
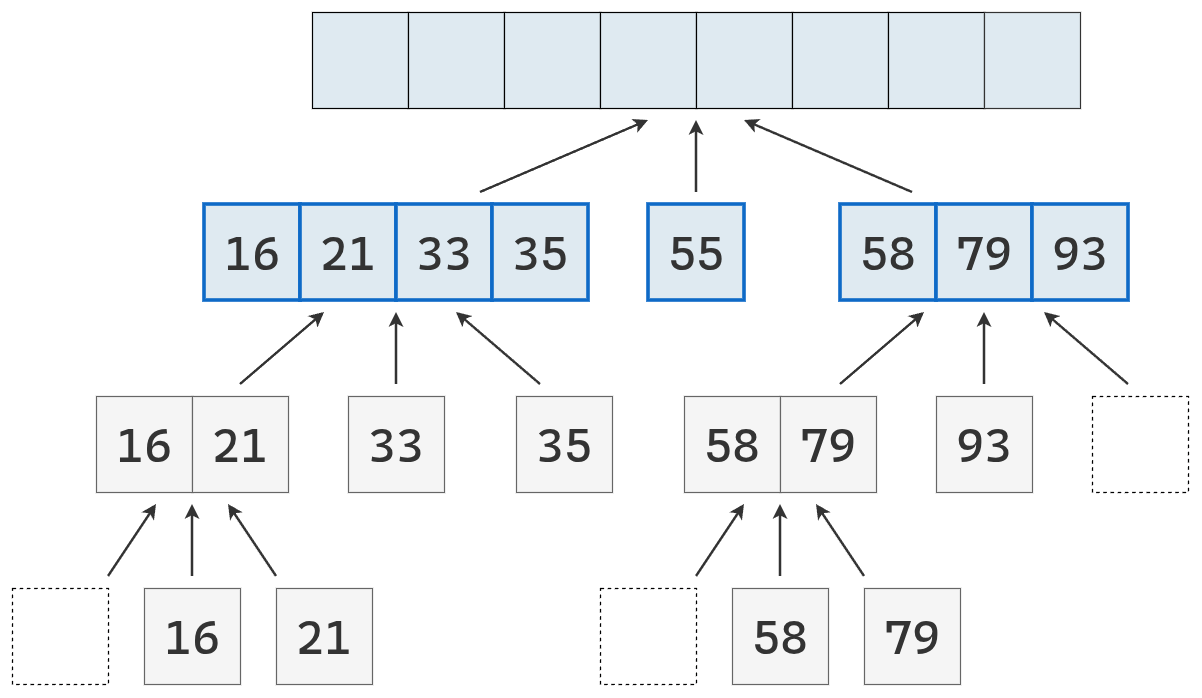
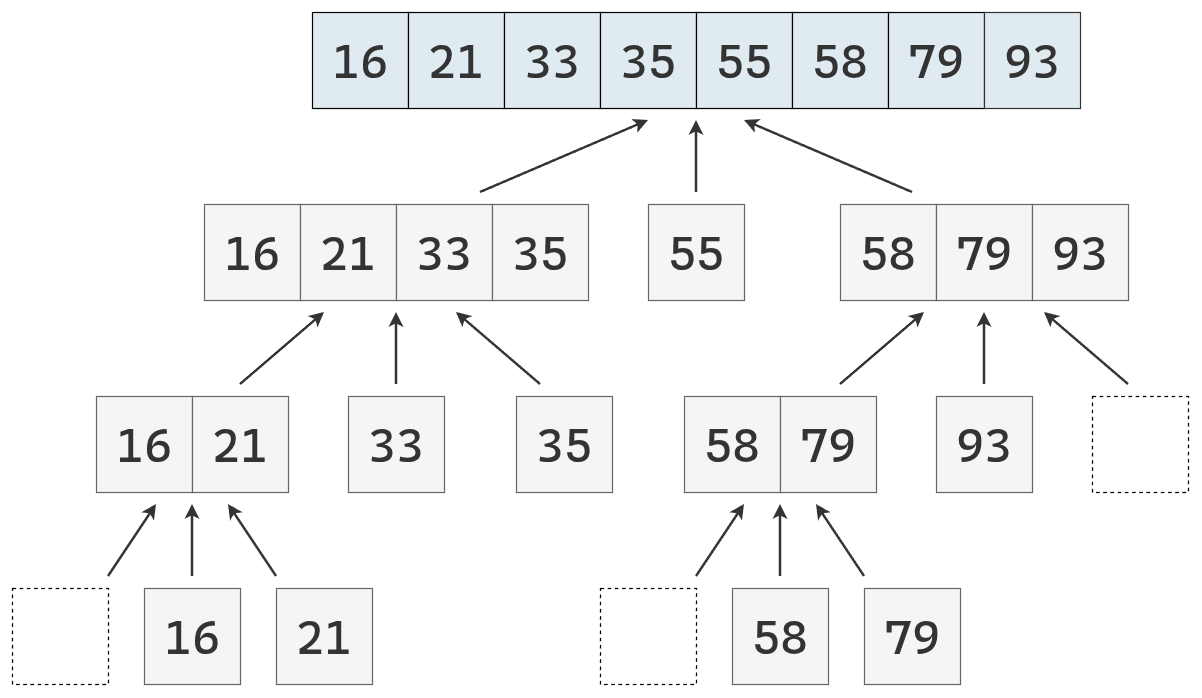
El siguiente conjunto de imágenes nos ayudarán a entender como fuciona merge sort de manera recursiva.
El algoritmo merge sort se basa principalmente en particiones y fusiones. Las particiones son sencillas de entender e implementar.
Por otro lado, no es trivial obtener una secuencia ordenada a partir de la fusión de dos secuencias también ordenadas. La operación excede a una simple concatenación.
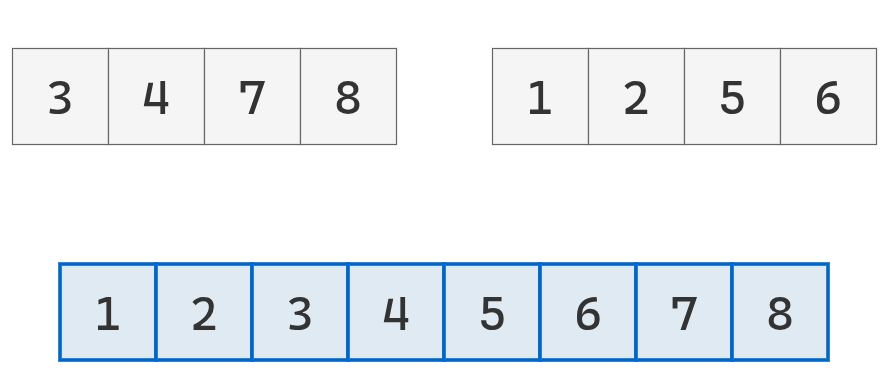
Para resolver este problema, merge sort usa un algoritmo conocido como fusión de arreglos (merging arrays). En este contexto, fusionar arreglos significa tomar dos arreglos que ya están ordenados, copiar todos sus valores en un tercer arreglo y obtener como resultado un tercer arreglo completamente ordenado.
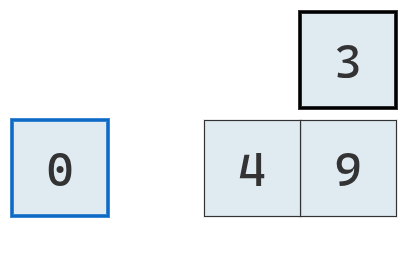
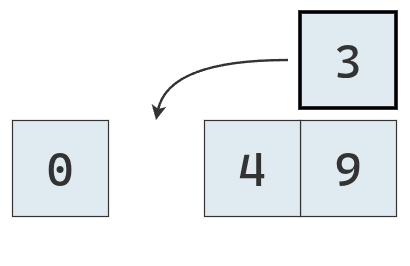
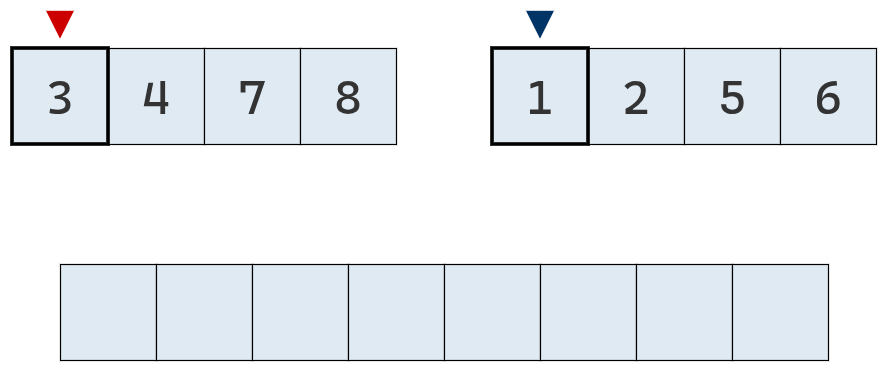
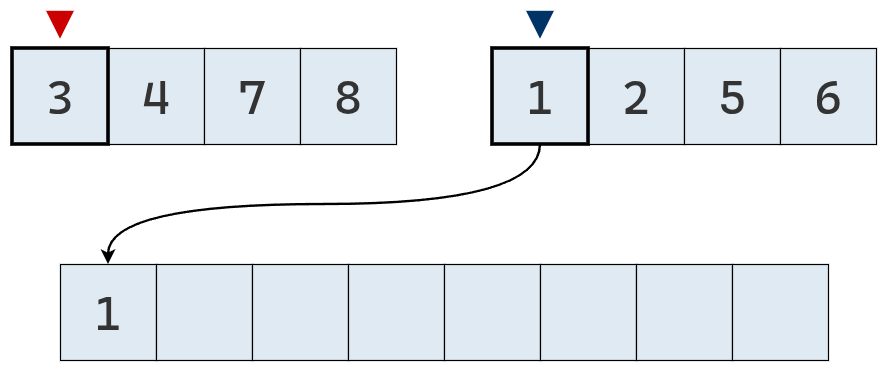
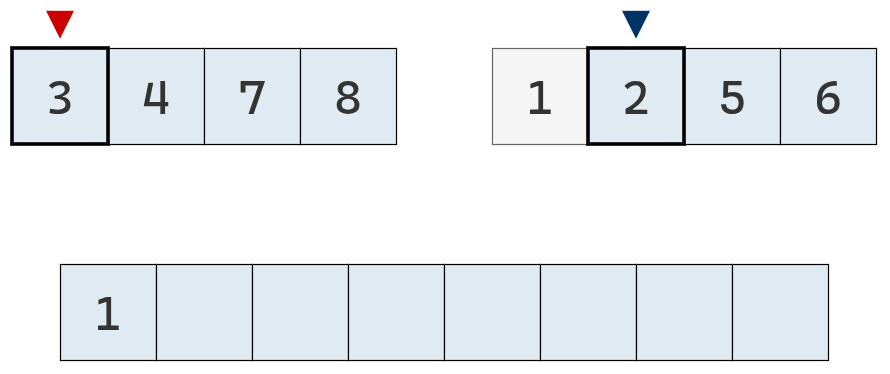
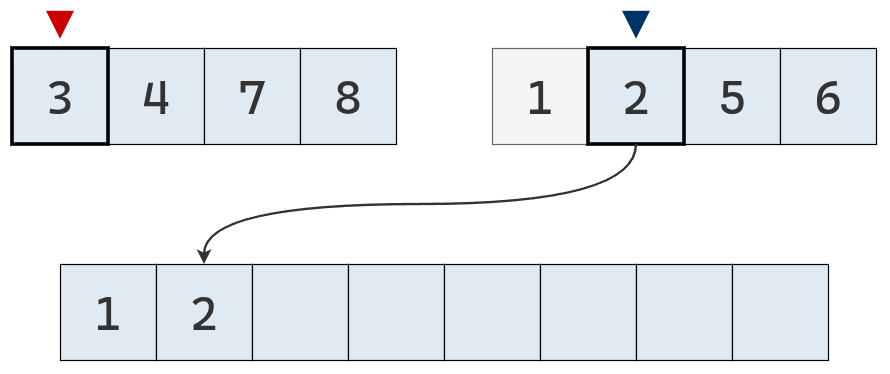
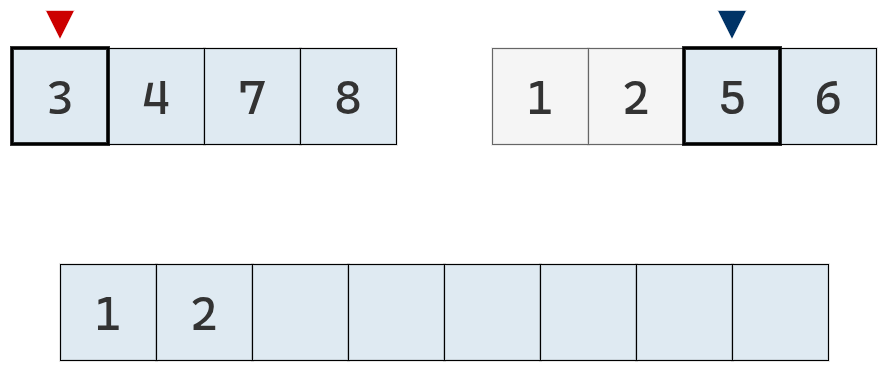
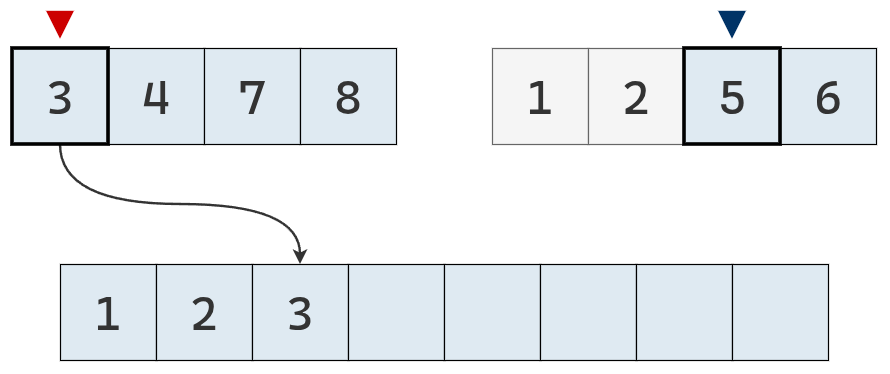
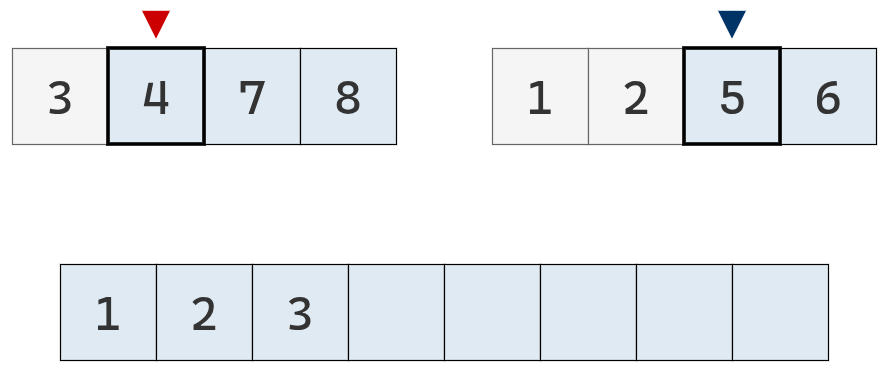
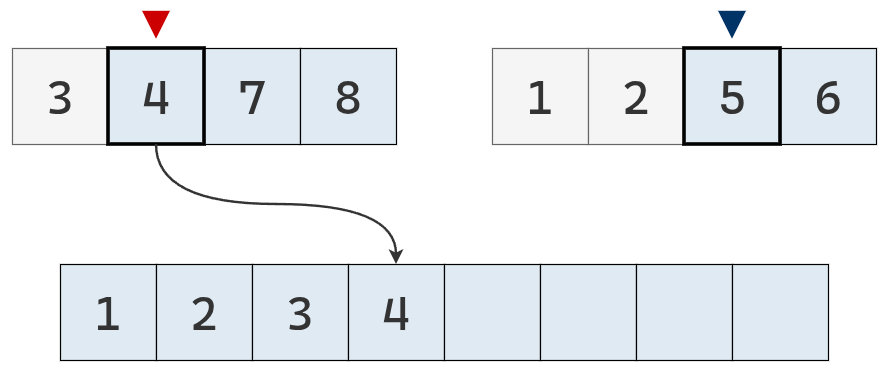
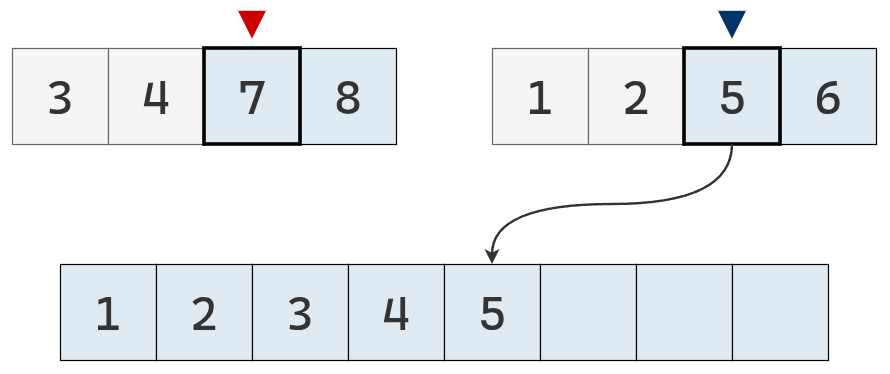
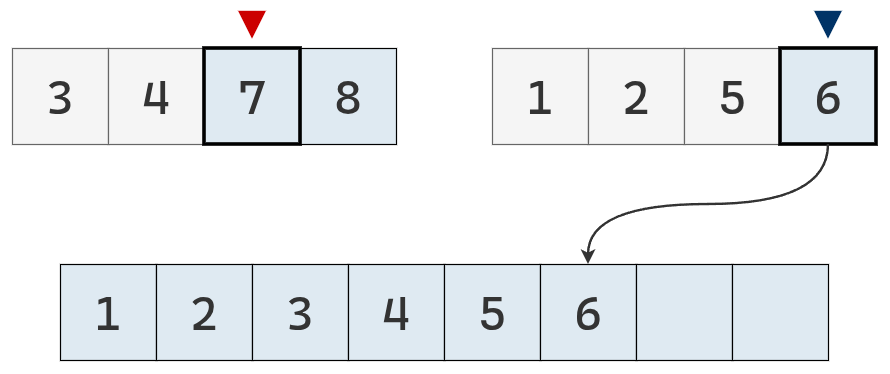
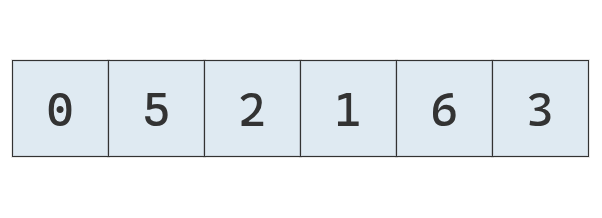
Para fusionar dos arreglos ordenados \(S_1\) y \(S_2\), el algoritmo de fusión sigue estos pasos:
- Se inicializa un puntero
izq, que apunta al primer índice de \(S_1\) , y otro punteroderque apunta al primer índice de \(S_2\). - Se crea un tercer arreglo vacío. Este será el arreglo con los datos fusionados, tendrá todos los valores de \(S_1\) y \(S_2\), en orden ascendente
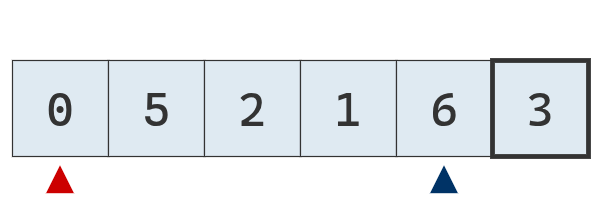
- Se ejecuta un bucle hasta que el puntero izquierdo o el puntero derecho lleguen al final de su respectivas secuencias. Dentro del bucle, realiza lo siguiente:
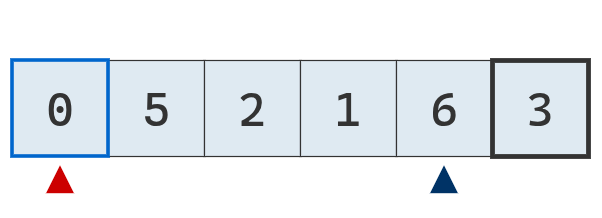
- Comparar el valor apuntado por el puntero izquierdo con el valor apuntado por el puntero derecho y determina cuál es menor.
- Tomar el valor menor y añadirlo al arreglo
fusionado. - Incrementar el puntero que estaba apuntando al valor menor para que señale el siguiente índice de su arreglo. Si en algún momento los dos valores que se comparan son iguales, se puede añadir arbitrariamente el valor del arreglo
izqe incrementar su puntero.
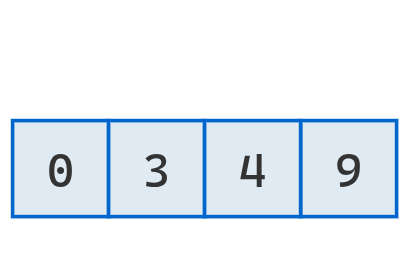
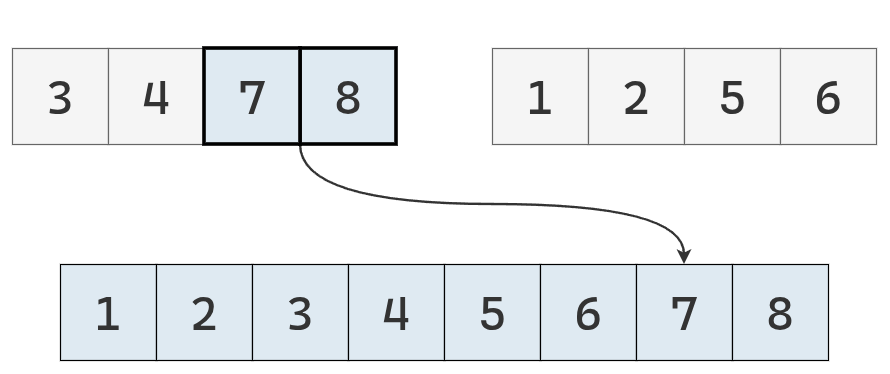
- Una vez que el bucle termina, uno de los dos arreglos (\(S_1\) o \(S_2\)) quedará “incompleto”, es decir, aún tendrá valores que no se copiaron al arreglo
fusionado. Esto da inicio al último paso del algoritmo. - Se toman todos los valores restantes del arreglo “incompleto” y es añaden, en orden, al arreglo
fusionado.
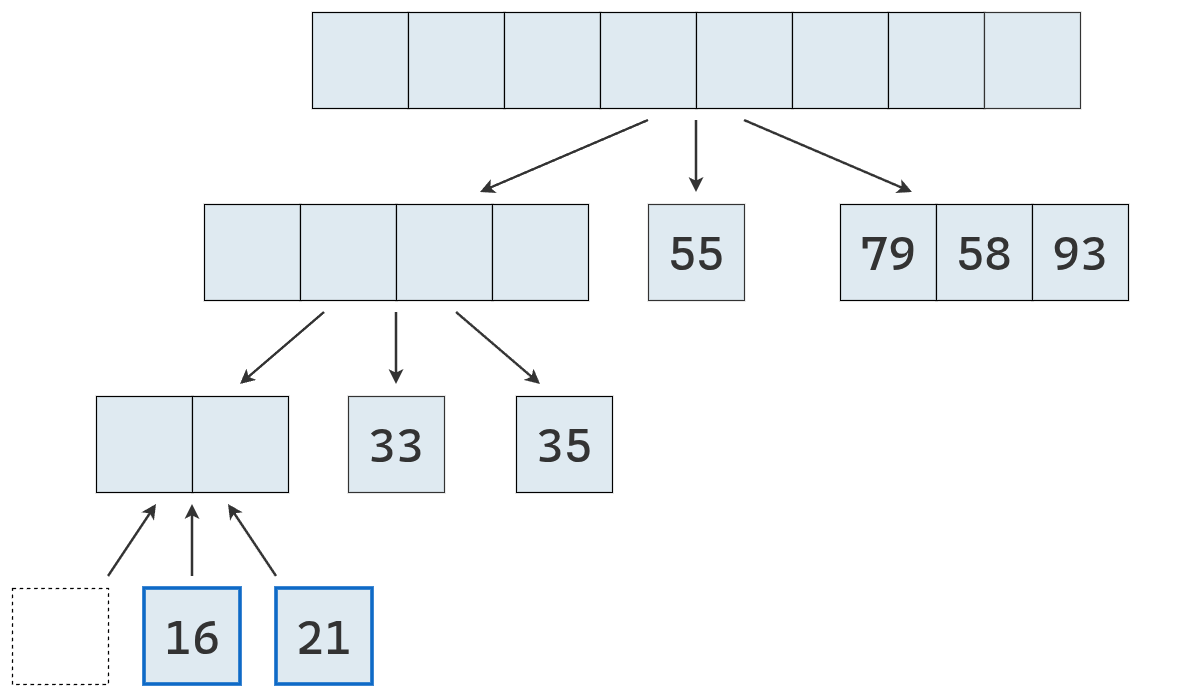
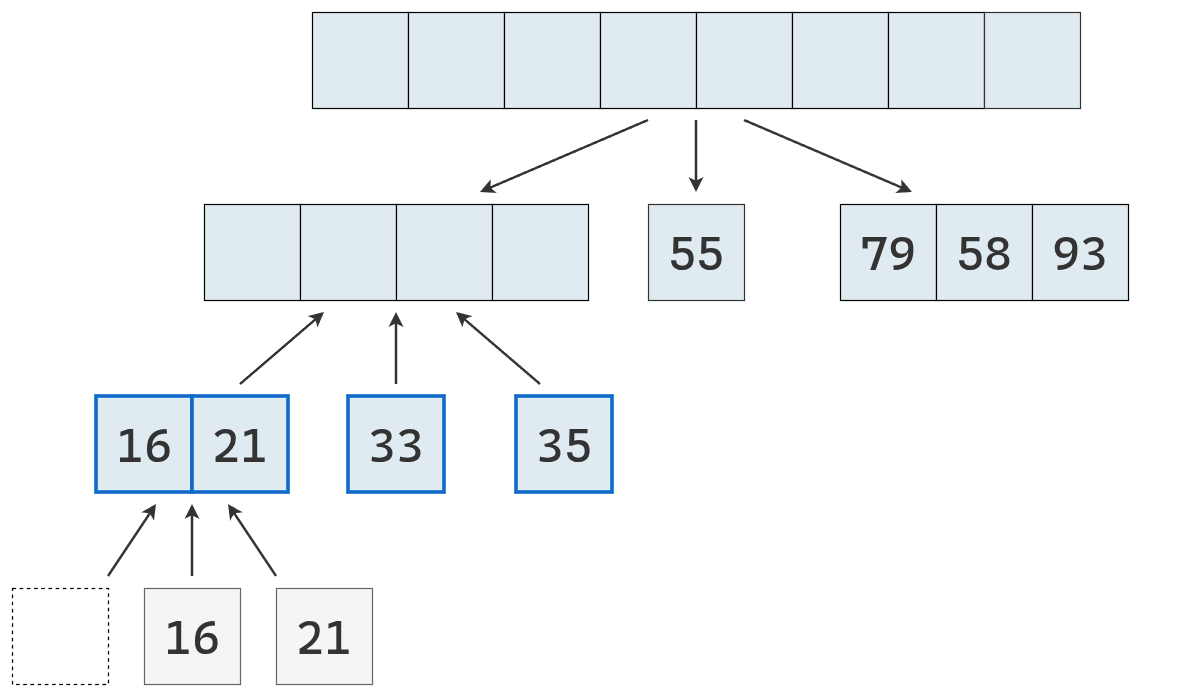
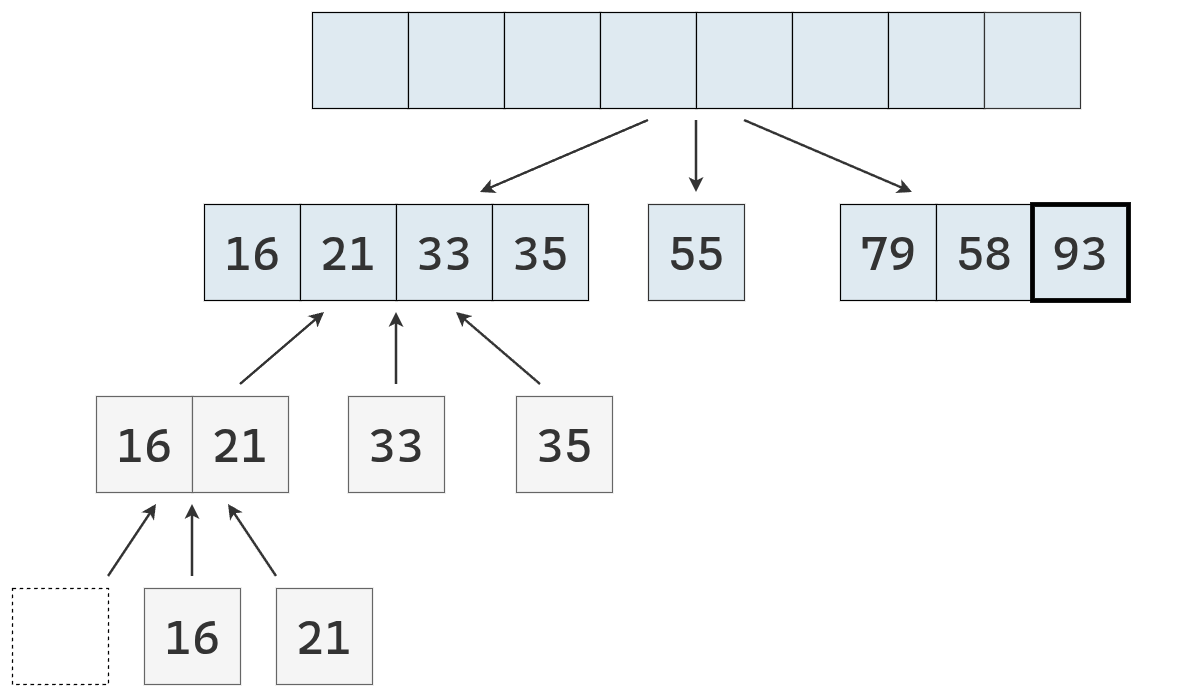
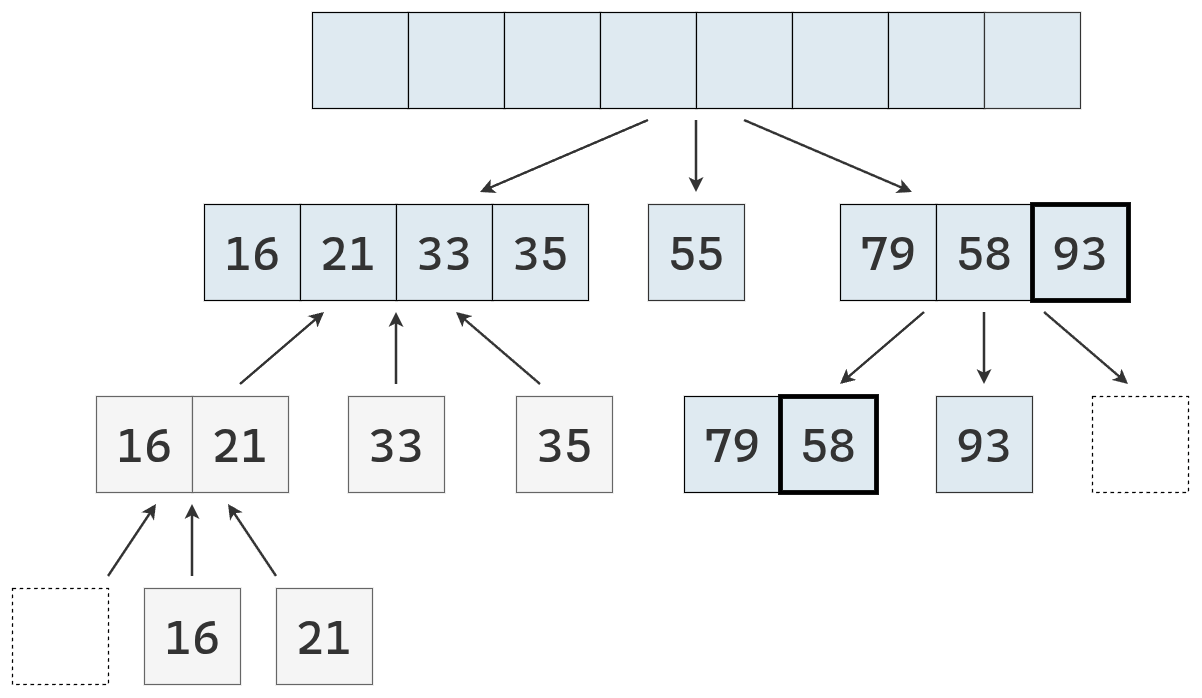
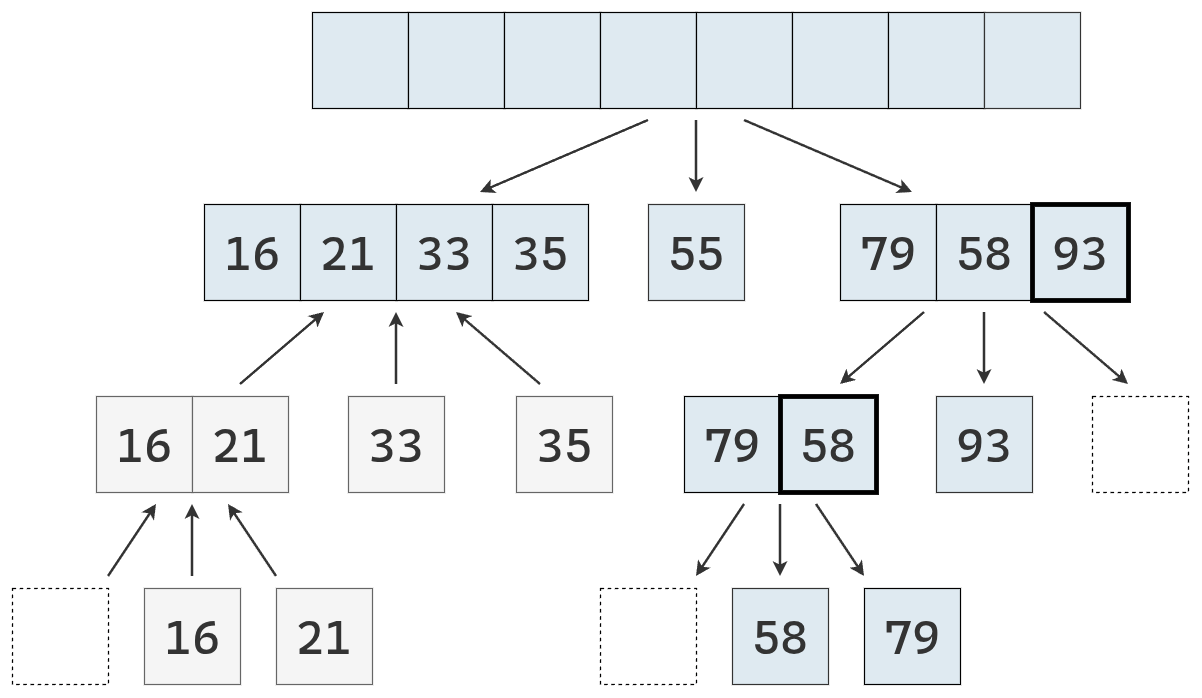
Veamos el ejemplo desarrollado paso a paso:
Implementación
Una implementación en Python es la siguiente:
def merge(izquierda, derecha):
n_i = len(izquierda)
n_j = len(derecha)
resultado = [None] * (n_i + n_j)
i = 0
j = 0
k = 0
while True:
if izquierda[i] < derecha[j]:
valor = izquierda[i]
i += 1
else:
valor = derecha[j]
j += 1
resultado[k] = valor
k += 1
if i == n_i:
resultado[k:] = derecha[j:]
break
if j == n_j:
resultado[k:] = izquierda[i:]
break
return resultadoY luego, tenemos la función merge_sort:
def merge_sort(arr):
if len(arr) <= 1:
return arr
mitad = len(arr) // 2
izquierda = merge_sort(arr[:mitad])
derecha = merge_sort(arr[mitad:])
return merge(izquierda, derecha)merge([2, 2, 3, 11, 50], [3, 10, 15, 20])
# [2, 2, 3, 3, 10, 11, 15, 20, 50]merge_sort([50, 3, 10, 11, 20, 99, 155, 8, 5, 9])
# [3, 5, 8, 9, 10, 11, 20, 50, 99, 155]Hacer clic aquí.
La versión de merge sort que acabamos de ver se conoce como top-down, y utiliza recursión.
Sin embargo, no es la única forma de implementar este algoritmo. Existe también una versión llamada bottom-up, que no emplea recursión.
En la práctica, suele ser algo más eficiente, ya que evita mantener un stack de llamadas y la memoria asociada a cada una de ellas.
Análisis de eficiencia
El análisis de la complejidad de merge sort se basa en entender los dos procesos principales que componen el algoritmo:
- La división recursiva de la lista en mitades.
- La fusión (merge) de las sublistas ordenadas en una nueva lista.
El proceso de fusión
El corazón del algoritmo está en la operación de fusión, donde dos listas ordenadas se combinan en una sola lista también ordenada. Si consideramos que entre ambas listas hay un total de \(N\) elementos, entonces el proceso completo de fusión requiere, en el peor de los casos, alrededor de \(2N\) pasos:
- \(N\) operaciones para copiar los elementos en la lista final,
- y hasta \(N - 1\) comparaciones para decidir el orden en que se insertan.
Al sumar ambos tipos de operaciones, tenemos un total de \(2N - 1\) pasos, que en notación Big O se escribe como \(O(N)\). En otras palabras, fusionar dos listas ordenadas es una operación de complejidad lineal.
El número de divisiones
Ahora bien, merge sort no realiza una única fusión. El algoritmo divide recursivamente la lista original en mitades, aplicando el mismo proceso a cada parte. Cada división parte la lista en dos, y la cantidad máxima de veces que puede hacerse esto es proporcional al logaritmo del tamaño de la lista. Es decir, si la lista tiene \(N\) elementos, podemos dividirla como mucho \(\log_2 N\) veces, hasta que llegamos a sublistas de tamaño 1 (que ya están ordenadas por definición).
Combinando ambos procesos
En cada “nivel” de la recursión se realizan fusiones que, en conjunto, procesan todos los elementos de la lista. Por lo tanto, cada nivel tiene un costo de complejidad \(O(N)\), y como hay \(\log N\) niveles, el costo total del algoritmo es:
\[ O(N) \times O(\log N) = O(N \log N) \]
Esta complejidad temporal indica que merge sort es más eficiente, en cantidad de pasos, que todos los algoritmos que estudiamos previamente.
Complejidad espacial
La eficiencia en tiempo tiene un costo adicional, el uso de memoria. Durante la fusión, el algoritmo necesita espacio extra para almacenar las sublistas temporales que se van creando y combinando. Esto implica una complejidad espacial de \(O(N)\), ya que se debe reservar memoria proporcional al tamaño total de la lista.
Quick sort
El algoritmo quick sort también se basa en el paradigma de dividir y conquistar. La idea es dividir la secuencia en partes más pequeñas, ordenarlas de forma recursiva y luego combinarlas mediante una simple concatenación.
Versión básica
El algoritmo puede describirse en tres pasos:
- Dividir: se elige un elemento de la secuencia, llamado pivote. En la práctica, suele seleccionarse el último elemento o uno al azar (que se mueve al final). Luego, se recorre la secuencia y se distribuyen sus elementos en tres nuevas subsecuencias:
- \(L\): que contiene los valores menores que el pivote.
- \(E\): que contiene los valores iguales al pivote.
- \(G\): que contiene los valores mayores que el pivote.
- Conquistar: se ordenan recursivamente las subsecuencias \(L\) y \(G\), aplicando el mismo procedimineto
- Combinar: se unen las subsecuencias en una sola secuencia ordenada, concatenando los elementos de \(L\), \(E\) y \(G\) en ese orden.
En Python:
def quicksort_basico(arr):
if len(arr) <= 1:
return arr
pivote = arr[-1]
menores = []
iguales = []
mayores = []
for x in arr:
if x < pivote:
menores.append(x)
elif x == pivote:
iguales.append(x)
else:
mayores.append(x)
return quicksort_basico(menores) + iguales + quicksort_basico(mayores)quicksort_basico([33, 1, 2, 5, 4, 3, 20, 10])
# [1, 2, 3, 4, 5, 10, 20, 33]Esta versión es conceptualmente sencilla, pero utiliza memoria adicional para almacenar las tres subsecuencias creadas en cada paso recursivo.
Versión in place
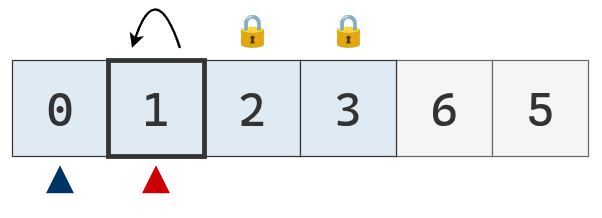
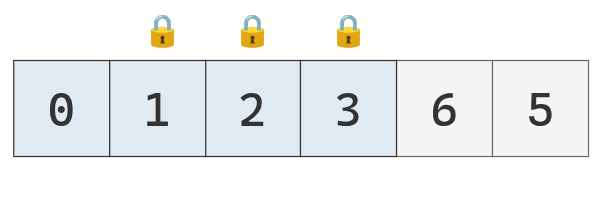
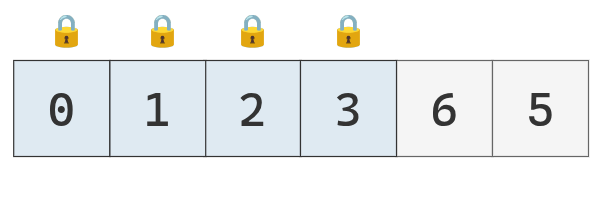
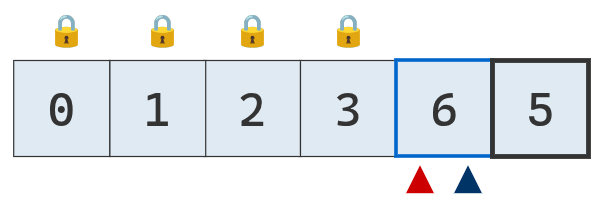
Existe otra implementación, más eficiente en el uso de memoria, conocida como versión in place. En lugar de crear nuevas subsecuencias, modifica la secuencia original intercambiando elementos de lugar. En ese sentido, se asemeja a algoritmos como bubble sort, selection sort o insertion sort.
La partición se realiza utilizando dos punteros, izq y der, que comienzan en los extremos de la parte de la secuencia que se está procesando, luego de haber seleccionado el pivote.
- El puntero
izqavanza hacia la derecha hasta encontrar un valor mayor o igual al pivote. - El puntero
deravanza hacia la izquierda hasta encontrar un valor menor o igual al pivote.
Cuando ambos punteros se detienen:
- Si no se han cruzado, se intercambian los valores y el proceso se repite.
- Si se cruzan, se intercambia el pivote con el elemento apuntado por
izq.
En ese momento se completa una partición: los valores menores al pivote quedan a su izquierda y los mayores, a su derecha. Luego, el algoritmo se aplica recursivamente sobre cada una de las dos partes resultantes.
El proceso que acabamos de describir es una partición. El valor del pivote ahora se encuentra en su lugar definitivo en la lista ordenada. Ahora, el algoritmo quick sort particiona recursivamente las secciones restantes.
Implementación
def _quick_sort(arr, inicio, fin):
"""Ordena la lista 'arr' _in place_ usando el algoritmo quicksort."""
if fin - inicio <= 0:
return
# Realizar la partición y obtener la posición final del pivote
pivote_idx = particionar(arr, inicio, fin)
# Ordenar recursivamente las dos mitades
_quick_sort(arr, inicio, pivote_idx - 1)
_quick_sort(arr, pivote_idx + 1, fin)
def particionar(arr, izq_idx, der_idx):
pivote_idx = der_idx
pivote = arr[pivote_idx]
der_idx -= 1
while True:
while arr[izq_idx] < pivote:
izq_idx += 1
while arr[der_idx] > pivote:
der_idx -= 1
if izq_idx >= der_idx:
break
else:
arr[izq_idx], arr[der_idx] = arr[der_idx], arr[izq_idx]
izq_idx += 1
# Finalizar particion
arr[izq_idx], arr[pivote_idx] = arr[pivote_idx], arr[izq_idx]
return izq_idx
def quick_sort(arr):
arr_copia = arr[:]
_quick_sort(arr_copia, inicio=0, fin=len(arr) - 1) # Ordena _in place_
return arr_copiaquick_sort([8, 3, 1, 7, 0, 10, 2])
# [0, 1, 2, 3, 7, 8, 10]Hacer clic aquí.
Análisis de eficiencia
El costo de quick sort proviene principalmente del proceso de partición, en el que cada elemento de la lista se compara con el pivote.
Se realizan unas \(N\) comparaciones por partición y un número menor de intercambios, ya que cada intercambio reubica dos elementos a la vez.
Por lo tanto, una partición completa cuesta tiene una complejidad de orden \(O(N)\).
En el mejor escenario, los pivotes dividen la lista en mitades iguales. Primero se hacen particiones de tamaño \(N\), luego de \(N/2\), luego de \(N/4\), y así sucesivamente, hasta llegar a sublistas de un solo elemento. Eso genera \(\log N\) niveles de partición, y como cada nivel cuesta \(O(N)\) el tiempo total resulta \(O(N \log N)\).
En el peor caso, los pivotes dividen la lista de manera muy desbalanceada, por ejemplo cuando siempre se elige como pivote el elemento más pequeño o el más grande. En ese caso, después de ordenar un pivote, queda una sublista con \(N-1\) elementos, luego otra con \(N-2\), y así hasta llegar a 1. El número total de operaciones forma la suma \(N + (N-1) + (N-2) + \dots + 1\), que equivale a \(O(N^2)\).
Respecto al espacio, la versión in place no crea nuevas listas; todo se hace dentro de la secuencia original. Sin embargo, cada llamada recursiva debe mantenerse en la pila de ejecución mientras espera que terminen las llamadas siguientes. Como la profundidad de la recursión depende de la altura del árbol de particiones (a lo sumo \(\log N\) en promedio), el uso de memoria adicional es \(O(\log N)\).
Resumen
Los primeros algoritmos de ordenamiento, como bubble sort, selection sort e insertion sort, son sencillos de entender e implementar, pero presentan una complejidad temporal cuadrática, \(O(N^2)\). Esto significa que el número de pasos necesarios crece de manera proporcional al cuadrado de la cantidad de elementos a ordenar. En consecuencia, cuando el tamaño de la lista aumenta, el tiempo de ejecución se vuelve rápidamente impráctico. Aun así, estos algoritmos son útiles para introducir los fundamentos del análisis de eficiencia y para comprender las diferencias entre comparaciones, intercambios y desplazamientos.
Para superar esas limitaciones, surgieron algoritmos más sofisticados basados en el paradigma de dividir y conquistar, como merge sort y quick sort. Ambos logran reducir la complejidad temporal promedio a \(O(N \log N)\) al dividir el problema en partes más pequeñas, ordenarlas por separado y luego combinarlas. Esta mejora implica que el número de operaciones crece mucho más lentamente con el tamaño del conjunto de datos, lo que los hace adecuados para ordenar listas grandes.
Sin embargo, la mayor eficiencia en tiempo suele implicar un costo en memoria. Merge sort, por ejemplo, necesita espacio adicional para almacenar las sublistas temporales generadas durante el proceso de fusión, lo que le otorga una complejidad espacial de \(O(N)\). Quick sort, en cambio, puede implementarse in place, sin crear nuevas listas, pero requiere cierta cantidad de memoria para mantener las llamadas recursivas en la pila de ejecución. Así, elegir un algoritmo no depende solo de su velocidad, sino también de los recursos disponibles y del tipo de datos a procesar.
En síntesis, los algoritmos más simples son didácticos y apropiados para listas pequeñas o casi ordenadas, mientras que los más complejos ofrecen un desempeño muy superior en escenarios reales. Comprender sus ventajas y limitaciones permite tomar decisiones más informadas al momento de seleccionar el método de ordenamiento adecuado para cada situación.